En este tema
Ajuste
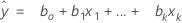
Notación
| Término | Description |
|---|---|
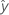 | valor ajustado |
| xk | késimo término. Cada término puede ser un solo predictor, un término polinómico o un término de interacción. |
| k | estimación del késimo coeficiente de regresión |
Error estándar del valor ajustado (EE ajuste)
El error estándar del valor ajustado en un modelo de regresión con un predictor es:

El error estándar del valor ajustado en un modelo de regresión con más de un predictor es:

Para la regresión ponderada, incluya la matriz de peso en la ecuación:

Cuando los datos tienen un conjunto de datos de prueba o una validación cruzada k-fold, las fórmulas son las mismas. El valor de s2 es de los datos de entrenamiento. La matriz de diseño y la matriz de peso también provienen de los datos de entrenamiento.
Notación
| Término | Description |
|---|---|
| s2 | mean square error |
| n | number of observations |
| x0 | new value of the predictor |
 | mean of the predictor |
| xi | i-ésimo predictor value |
| x0 | vector of values that produce the fitted values, one for each column in the design matrix, beginning with a 1 for the constant term |
| x'0 | transpose of the new vector of predictor values |
| X | design matrix |
| W | weight matrix |
Residuos
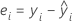
Notación
| Término | Description |
|---|---|
| yi | valor de la iésima respuesta observada |
 | iésimo valor ajustado para la respuesta |
Residuo estandarizado (Residuo est.)
Los residuos estandarizados también se denominan residuos "studentizados internamente".
Fórmula

Notación
| Término | Description |
|---|---|
| ei | i ésimo residuo |
| hi | i ésimo elemento diagonal de X(X'X)–1X' |
| s2 | cuadrado medio del error |
| X | matriz de diseño |
| X' | transpuesta de la matriz de diseño |
Residuos eliminados (studentizados)
También conocidos como residuos studentizados externamente. La fórmula es:
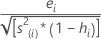
Otra presentación de esta fórmula es:

El modelo que estima la iésima observación, omite la iésimaobservación del conjunto de datos. Por lo tanto, la iésima observación no puede influir en la estimación. Cada residuo eliminado tiene una distribución t de Student con 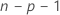 grados de libertad.
grados de libertad.
Notación
| Término | Description |
|---|---|
| ei | iésimo residuo |
| s(i)2 | cuadrado medio del error calculado sin la iésima observación |
| hi | iésimo elemento diagonal de X(X'X)–1X' |
| n | número de observaciones |
| p | número de términos, incluyendo la constante |
| SSE | suma de los cuadrados para el error |
Intervalo de confianza
El rango en el que se espera que se encuentre la respuesta media estimada para un conjunto dado de valores de predictor.
Fórmula
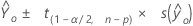
Notación
| Término | Description |
|---|---|
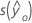 |  |
 | valor de respuesta ajustado para un conjunto dado de valores de predictor |
| α | tasa de error de tipo I |
| n | número de observaciones |
| p | número de parámetros del modelo |
| S 2(b) | matriz de varianzas-covarianzas de los coeficientes |
| s 2 | cuadrado medio del error |
| X | matriz de diseño |
| X0 | vector de valores dados de predictor con 1 columna y p filas |
| X'0 | transposición del nuevo vector de valores de predictor con 1 fila y p columnas |
Intervalo de predicción
El intervalo de predicción es el rango en el que se espera que se encuentre la respuesta ajustada para una nueva observación.
Fórmula
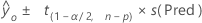
Notación
| Término | Description |
|---|---|
| s(Pred) |  |
 | valor de respuesta ajustado para un conjunto dado de valores predictores |
| α | nivel de significancia |
| n | número de observaciones |
| p | número de parámetros del modelo |
| s 2 | cuadrado medio del error |
| X | matriz de predictores |
| X0 | vector de valores dados de predictor con 1 columna y p filas |
| X'0 | transposición del nuevo vector de valores de predictor con 1 fila y p columnas |
