En este tema
Probabilidad observada
La probabilidad observada es el número de eventos dividido entre el número de ensayos. Por ejemplo, cuando el número de eventos es 30 y el número de ensayos es 495, entonces la probabilidad observada es 0.06061.
Ajuste
El valor ajustado también se conoce como la probabilidad del evento o la probabilidad pronosticada. La probabilidad del evento es la probabilidad de que ocurra el evento experimental especificado. La probabilidad del evento estima la probabilidad de que ocurra un evento, como sacar un as de un mazo de cartas o producir una pieza no conforme. La probabilidad de un evento varía de 0 (imposible) a 1 (seguro).
Interpretación
La respuesta experimental solo tiene dos valores posibles, como la presencia o ausencia de una enfermedad particular. La probabilidad del evento es la probabilidad de que ocurra la respuesta para un patrón dado de factores o covariables (por ejemplo, la probabilidad de que una mujer mayor de 50 años desarrolle diabetes tipo 2).
Cada ejecución en un experimento se denomina ensayo. Por ejemplo, si usted lanza una moneda al aire 10 veces y registra el número de caras, usted realiza 10 ensayos del experimento. Si los ensayos son independientes e igual de probables, usted puede estimar la probabilidad del evento dividiendo el número de eventos entre el número total de ensayos. Por ejemplo, si obtiene 6 caras en 10 lanzamientos de moneda, la probabilidad estimada del evento (obtener caras) es:
Número de eventos ÷ Número de ensayos = 6 ÷ 10 = 0,6
EE ajuste
El error estándar del ajuste (EE ajuste) estima la variación en la probabilidad del evento para la configuración especificada de las variables. El cálculo del intervalo de confianza para la probabilidad del evento utiliza el error estándar del ajuste. Los errores estándar son siempre no negativos.
Interpretación
Utilice el error estándar del ajuste para medir la precisión de la estimación de la probabilidad del evento. Cuanto menor sea el error estándar, más precisa será la respuesta media pronosticada.
Por ejemplo, un investigador estudia los factores que afectan la inclusión en un estudio médico. Para un conjunto factores, la probabilidad de que un paciente califique para ser incluido en un estudio para un nuevo tratamiento es 0.63, con un error estándar de 0.05. Para un segundo conjunto de valores de configuración de los factores, la probabilidad es la misma, pero con un error estándar del ajuste de 0.03. El analista puede estar más seguro de que la probabilidad del evento del segundo conjunto de valores de configuración de las variables está cerca de 0.63.
Intervalo de confianza para el ajuste (IC de 95%)
Estos intervalos de confianza (IC) son rangos de valores que es muy probable que contengan la probabilidad del evento para la población que incluye los valores observados de las variables predictoras que se encuentran en el modelo.
Puesto que las muestras son aleatorias, es poco probable que dos muestras de una población produzcan intervalos de confianza idénticos. Sin embargo, si se toman muchas muestras, un determinado porcentaje de los intervalos de confianza resultantes incluirá el parámetro de población desconocido. El porcentaje de estos intervalos de confianza que contiene el parámetro es el nivel de confianza del intervalo.
- Estimación de punto
- La estimación de punto es la estimación del parámetro que se calcula a partir de los datos de la muestra.
- Margen de error
- El margen de error define la amplitud del intervalo de confianza y se ve afectado por el rango de probabilidades del evento, el tamaño de la muestra y el nivel de confianza.
Interpretación
Utilice el intervalo de confianza para evaluar la estimación del valor ajustado para los valores observados de las variables.
Por ejemplo, con un nivel de confianza de 95%, usted puede estar 95% seguro de que el intervalo de confianza contiene la probabilidad del evento para los valores especificados de las variables incluidas en el modelo. El intervalo de confianza ayuda a evaluar la significancia práctica de los resultados. Utilice su conocimiento especializado para determinar si el intervalo de confianza incluye valores que tienen significancia práctica para su situación. Si el intervalo es demasiado amplio para ser útil, considere aumentar el tamaño de la muestra.
Resid
El residuo es una medida de qué tan bien el modelo pronostica la observación. Por opción predeterminada, Minitab calcula los residuos de desviación. Las observaciones que el modelo no ajusta adecuadamente tienen altos residuos de desviación y de Pearson. Minitab calcula los residuos para cada patrón diferente de factores/covariables.
La interpretación de los residuos es igual si se usan los residuos de desviación o los residuos de Pearson. Cuando el modelo usa la función de enlace logit, la distribución de los residuos de desviación está más cerca de la distribución de los residuos de un modelo de regresión de mínimos cuadrados. Los residuos de desviación y los residuos de Pearson se vuelven más similares a medida que aumenta el número de ensayos para cada combinación de valores de configuración de los predictores.
Interpretación
Grafique los residuos para determinar si el modelo es adecuado y cumple con los supuestos de regresión. Examinar los residuos puede ofrecer información útil acerca de qué tan bien se ajusta el modelo a los datos. En general, los residuos deberían estar distribuidos aleatoriamente, sin patrones obvios ni valores poco comunes. Si Minitab determina que los datos incluyen observaciones poco comunes, identifica esas observaciones en la tabla Ajustes y diagnósticos para observaciones poco comunes en la salida. Para obtener más información sobre valores poco comunes, vaya a Observaciones poco comunes.
Resid Est
El residuo estandarizado es igual al valor de un residuo (ei) dividido entre una estimación de su desviación estándar.
Interpretación
Utilice los residuos estandarizados como ayuda para detectar valores atípicos. Los residuos estandarizados mayores que 2 y menores que −2 por lo general se consideran grandes. La tabla Ajustes y diagnósticos para observaciones poco comunes identifica estas observaciones con una 'R'. Cuando un análisis indica que hay muchas observaciones poco comunes, el modelo generalmente exhibe una falta de ajuste significativa. Es decir, el modelo no describe adecuadamente la relación entre los factores y la variable de respuesta. Para obtener más información, vaya a Observaciones poco comunes.
Los residuos estandarizados son útiles porque los residuos sin procesar podrían no ser buenos indicadores de valores atípicos. La varianza de cada residuo sin procesar puede diferir según los valores de X asociados al residuo. Esta escala desigual hace que sea difícil evaluar los tamaños de los residuos sin procesar. La estandarización de los residuos soluciona este problema al convertir las diferentes varianzas a una escala común.
La interpretación de los residuos es igual si se usan los residuos de desviación o los residuos de Pearson. Cuando el modelo usa la función de enlace logit, la distribución de los residuos de desviación está más cerca de la distribución de los residuos de un modelo de regresión de mínimos cuadrados. Los residuos de desviación y los residuos de Pearson se vuelven más similares a medida que aumenta el número de ensayos para cada combinación de valores de configuración de los predictores.
Residuos elim.
Cada residuo studentizado eliminado se calcula con una fórmula que equivale a eliminar sistemáticamente cada una de las observaciones del conjunto de datos, estimar la ecuación de regresión y determinar qué tan bien el modelo predice la observación eliminada. Cada residuo studentizado eliminado también se estandariza al dividir el residuo eliminado de una observación entre una estimación de su desviación estándar. La observación se omite para determinar cómo se comporta el modelo sin esta observación. Si una observación tiene un residuo eliminado studentizado grande (si su valor absoluto es mayor que 2), podría tratarse de un valor atípico en los datos.
Interpretación
Utilice los residuos studentizados eliminados para detectar valores atípicos. Cada observación se omite para determinar qué tan bien el modelo predice la respuesta cuando no está incluida en el proceso de ajuste del modelo. Los residuos studentizados eliminados mayores que 2 o menores que −2 generalmente se consideran grandes. Las observaciones que Minitab etiqueta no siguen adecuadamente la ecuación de regresión propuesta. Sin embargo, se espera que haya algunas observaciones poco comunes. Por ejemplo, con base en los criterios para los residuos grandes, se esperaría que aproximadamente el 5% de las observaciones sean marcadas como observaciones con un residuo grande. Si el análisis revela muchas observaciones poco comunes, el modelo probablemente no describe adecuadamente la relación entre los predictores y la variable de respuesta. Para obtener más información, vaya a Observaciones poco comunes.
Los residuos estandarizados y eliminados podrían ser más útiles que los residuos sin procesar en la identificación de valores atípicos. Se ajustan a las posibles diferencias en la varianza de residuos sin procesar debido a los diferentes valores de los predictores o factores.
Hi (apalancamiento)
Hi, también conocido como apalancamiento, mide la distancia desde el valor de X de una observación hasta el promedio de los valores de X de todas las observaciones de un conjunto de datos.
Interpretación
Los valores de Hi están entre 0 y 1. Minitab identifica las observaciones con valores de apalancameinto superior a 3p/n o 99, el valor que sea menor, con una X en la tabla Ajustes y diagnósticos de observaciones poco comunes. En 3p/n, p es el número de coeficientes en el modelo y n es el número de observaciones. Las observaciones que Minitab etiqueta con una 'X' podrían ser influyentes.
Las observaciones influyentes tienen un efecto desproporcionado sobre el modelo y pueden producir resultados engañosos. Por ejemplo, la inclusión o exclusión de un punto influyente puede cambiar el hecho de si un coeficiente es estadísticamente significativo o no.. Las observaciones influyentes pueden ser puntos de apalancamiento, valores atípicos o ambos.
Si ve una observación influyente, determine si la observación es un error de entrada de datos o de medición. Si la observación no es un error de entrada de datos ni de medición, determine qué tan influyente es la observación. En primer lugar, ajuste el modelo con y sin la observación. Luego, compare los coeficientes, los valores p, el R2 y otras informaciones del modelo. Si el modelo cambia significativamente al eliminar la observación influyente, examine más a fondo el modelo para determinar si se especificó de forma incorrecta. Es posible que tenga que recopilar más datos para resolver el problema.
Distancia de Cook (D)
La distancia de Cook (D) mide el efecto que tiene una observación sobre el conjunto de coeficientes en un modelo lineal. La distancia de Cook considera tanto el valor de apalancamiento como el residuo estandarizado de cada observación para determinar el efecto de la observación.
Interpretación
Las observaciones con una D grande pueden ser consideradas influyentes. Un criterio comúnmente utilizado para un valor D grande es cuando D es mayor que la mediana de la distribución F: F(0.5, p, n-p), donde p es el número de términos del modelo, incluyendo la constante, y n es el número de observaciones. Otra manera de examinar los valores D consiste en compararlos entre sí, utilizando una gráfica, como una gráfica de valores individuales. Las observaciones con valores D que sean grandes en comparación con los demás valores podrían ser influyentes.
Las observaciones influyentes tienen un efecto desproporcionado sobre el modelo y pueden generar resultados engañosos. Por ejemplo, la inclusión o exclusión de un punto influyente puede cambiar el hecho de si un coeficiente es estadísticamente significativo o no.. Las observaciones influyentes pueden ser puntos de apalancamiento, valores atípicos o ambos.
Si ve una observación influyente, determine si la observación es un error de entrada de datos o de medición. Si la observación no es un error de entrada de datos ni de medición, determine qué tan influyente es la observación. En primer lugar, ajuste el modelo con y sin la observación. Luego, compare los coeficientes, los valores p, el R2 y otras informaciones del modelo. Si el modelo cambia significativamente al eliminar la observación influyente, examine más a fondo el modelo para determinar si se especificó de forma incorrecta. Es posible que tenga que recopilar más datos para resolver el problema.
DFITS
DFITS mide el efecto que tiene cada observación sobre los valores ajustados en un modelo lineal. DFITS representa aproximadamente el número de desviaciones estándar que el valor ajustado cambia cuando cada observación se elimina del conjunto de datos y se vuelve a ajustar el modelo.
Interpretación
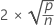
| Término | Description |
|---|---|
| p | el número de términos del modelo |
| n | el número de observaciones |
Si ve una observación influyente, determine si la observación es un error de entrada de datos o de medición. Si la observación no es un error de entrada de datos ni de medición, determine qué tan influyente es la observación. En primer lugar, ajuste el modelo con y sin la observación. Luego, compare los coeficientes, los valores p, el R2 y otras informaciones del modelo. Si el modelo cambia significativamente al eliminar la observación influyente, examine más a fondo el modelo para determinar si se especificó de forma incorrecta. Es posible que tenga que recopilar más datos para resolver el problema.
