Matriz de diseño
Minitab genera una matriz de diseño para cada diseño. La primera columna es una columna formada por números uno para el término constante. Si el diseño se dividió en k bloques, hay columnas (k - 1) para bloques. Minitab utiliza el mismo método de codificación de bloques que en los Modelos factoriales. Esto es seguido por una columna para cada efecto principal. Los términos con factores categóricos pueden tener más de una columna. Si el modelo tiene términos cuadrados, existe una columna para cada término cuadrado. La columna para un término cuadrado es el producto del factor correspondiente consigo mismo. Si el modelo tiene términos de interacción, existe una columna para cada término de interacción. Las interacciones que incluyen factores categóricos pueden tener más de una columna. La columna para un término de interacción es el producto de las dos columnas que se cruzan.
Si Minitab elimina algunos de los términos porque los datos no pueden sustentarlos, estos términos no se almacenan en la matriz de diseño. Las columnas almacenadas coinciden con los coeficientes que se muestran.
Coeficiente (Coef)
En términos de matriz, la fórmula que calcula el vector de coeficientes en el modelo es:

Notación
| Término | Description |
|---|---|
| X | matriz de diseño |
| Y | vector de respuestas |
Transformación de Box-Cox
La transformación de Box Cox selecciona los valores de lambda, como se muestra a continuación, que minimizan la suma de los cuadrados de los residuos. La transformación resultante es Y λ cuando λ ≠ 0 y ln(Y) cuando λ = 0. Cuando λ < 0, Minitab también multiplica la respuesta transformada por −1 para mantener el orden de la respuesta no transformada.
Minitab busca un valor óptimo entre −2 y 2. Los valores que estén fuera de este intervalo podrían no producir un mejor ajuste.
Las siguientes son algunas transformaciones comunes donde Y′ es la transformación de los datos Y:
| Valor de lambda (λ) | Transformación |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0.5 | Y′ = 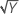 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0.5 |  |
| λ = −1 | Y′ = −1 / Y |
