Un ingeniero de empaques necesita cerciorarse de que los sellos de las bolsas de plástico que contienen un producto sean lo suficientemente fuertes como para evitar fugas, pero no tan fuertes como para que el consumidor no pueda abrir las bolsas. Las bolsas mantienen instrumentos quirúrgicos secos y estériles hasta que alguien abra las bolsas. El ingeniero desea optimizar la resistencia de los sellos entre 20 y 32 libras (límites superior e inferior) con un objetivo de 26 libras. También quiere minimizar la variabilidad en la resistencia de los sellos para que sea de 1 o menos. El ingeniero determina que la temperatura de la barra caliente, el tiempo de permanencia y la presión de la barra caliente son factores que afectan la resistencia del sello. Además, determina que la temperatura de la barra caliente, el tiempo de permanencia y la temperatura del material son factores importantes que afectan la variación. El ingeniero diseña un experimento central compuesto de superficie de respuesta para examinar los factores que afectan la resistencia y la variabilidad de los sellos. Usa la transformación del logaritmo natural para analizar la variabilidad del sello.
El ingeniero recolecta datos y analiza el diseño para determinar los factores que impactan la resistencia de sellado.
- Abra los datos de muestra, ResistSello.MWX.
- Elija .
- En Respuestas, ingrese Resistencia.
- Haga clic en Gráficas.
- En Gráficas de residuos, seleccione Cuatro en uno.
- Haga clic en Aceptar en cada cuadro de diálogo.
Interpretar los resultados
En la tabla Análisis de varianza, los valores p de HotBarT*HotBarT, DwelTime*DwelTime son significativos. El ingeniero puede reducir el modelo para eliminar los términos que no son significativos. Para obtener más información, vaya a Reducción del modelo.
El valor R2 muestra que el modelo explica un 78.58 % de la varianza en la resistencia, lo que indica que el modelo se ajusta adecuadamente bien a los datos. El R2 de 0 sugiere que este modelo está sobreajustado, lo que sustenta la reducción del modelo.
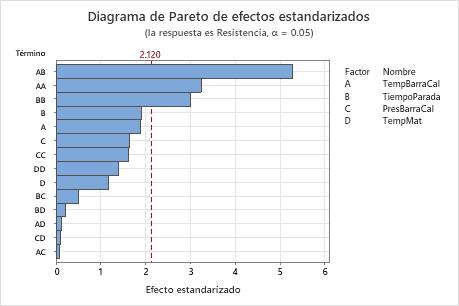
El diagrama de Pareto de los efectos permiten identificar visualmente los efectos importantes y comparar la magnitud relativa de los diversos efectos. Además, usted puede observar que el efecto más grande es la temperatura de la barra caliente y el tiempo de permanencia (AB), porque es el que más se extiende.
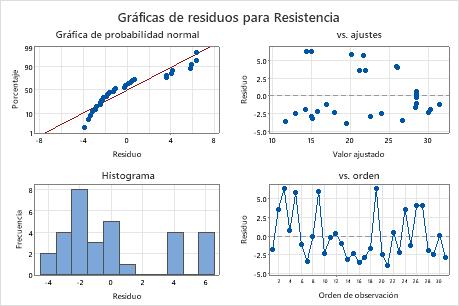
En las gráficas de residuos, los puntos en la gráfica de probabilidad normal no siguen la línea recta. La reducción del modelo puede ajustar esto.
Coeficientes codificados
| Término | Coef | EE del coef. | Valor T | Valor p | FIV |
|---|---|---|---|---|---|
| Constante | 28.44 | 1.66 | 17.09 | 0.000 | |
| TempBarraCal | 1.685 | 0.899 | 1.87 | 0.079 | 1.00 |
| TiempoParada | -1.719 | 0.899 | -1.91 | 0.074 | 1.00 |
| PresBarraCal | 1.481 | 0.899 | 1.65 | 0.119 | 1.00 |
| TempMat | 1.060 | 0.899 | 1.18 | 0.255 | 1.00 |
| TempBarraCal*TempBarraCal | -2.662 | 0.823 | -3.23 | 0.005 | 1.03 |
| TiempoParada*TiempoParada | -2.476 | 0.823 | -3.01 | 0.008 | 1.03 |
| PresBarraCal*PresBarraCal | -1.329 | 0.823 | -1.61 | 0.126 | 1.03 |
| TempMat*TempMat | -1.151 | 0.823 | -1.40 | 0.181 | 1.03 |
| TempBarraCal*TiempoParada | -5.81 | 1.10 | -5.28 | 0.000 | 1.00 |
| TempBarraCal*PresBarraCal | -0.09 | 1.10 | -0.08 | 0.938 | 1.00 |
| TempBarraCal*TempMat | -0.14 | 1.10 | -0.13 | 0.902 | 1.00 |
| TiempoParada*PresBarraCal | 0.55 | 1.10 | 0.50 | 0.624 | 1.00 |
| TiempoParada*TempMat | 0.24 | 1.10 | 0.22 | 0.832 | 1.00 |
| PresBarraCal*TempMat | -0.10 | 1.10 | -0.09 | 0.929 | 1.00 |
Resumen del modelo
| S | R-cuadrado | R-cuadrado(ajustado) | R-cuadrado (pred) |
|---|---|---|---|
| 4.40228 | 78.58% | 59.84% | 0.00% |
Análisis de Varianza
| Fuente | GL | SC Ajust. | MC Ajust. | Valor F | Valor p |
|---|---|---|---|---|---|
| Modelo | 14 | 1137.51 | 81.251 | 4.19 | 0.004 |
| Lineal | 4 | 218.65 | 54.662 | 2.82 | 0.060 |
| TempBarraCal | 1 | 68.13 | 68.129 | 3.52 | 0.079 |
| TiempoParada | 1 | 70.94 | 70.939 | 3.66 | 0.074 |
| PresBarraCal | 1 | 52.62 | 52.616 | 2.71 | 0.119 |
| TempMat | 1 | 26.96 | 26.963 | 1.39 | 0.255 |
| Cuadrado | 4 | 372.07 | 93.018 | 4.80 | 0.010 |
| TempBarraCal*TempBarraCal | 1 | 202.61 | 202.611 | 10.45 | 0.005 |
| TiempoParada*TiempoParada | 1 | 175.32 | 175.318 | 9.05 | 0.008 |
| PresBarraCal*PresBarraCal | 1 | 50.52 | 50.522 | 2.61 | 0.126 |
| TempMat*TempMat | 1 | 37.87 | 37.866 | 1.95 | 0.181 |
| Interacción de 2 factores | 6 | 546.79 | 91.132 | 4.70 | 0.006 |
| TempBarraCal*TiempoParada | 1 | 540.47 | 540.470 | 27.89 | 0.000 |
| TempBarraCal*PresBarraCal | 1 | 0.12 | 0.121 | 0.01 | 0.938 |
| TempBarraCal*TempMat | 1 | 0.30 | 0.305 | 0.02 | 0.902 |
| TiempoParada*PresBarraCal | 1 | 4.84 | 4.840 | 0.25 | 0.624 |
| TiempoParada*TempMat | 1 | 0.90 | 0.899 | 0.05 | 0.832 |
| PresBarraCal*TempMat | 1 | 0.16 | 0.160 | 0.01 | 0.929 |
| Error | 16 | 310.08 | 19.380 | ||
| Falta de ajuste | 10 | 308.20 | 30.820 | 98.51 | 0.000 |
| Error puro | 6 | 1.88 | 0.313 | ||
| Total | 30 | 1447.60 |
Ecuación de regresión en unidades no codificadas
| Resistencia | = | -289.3 + 2.287 TempBarraCal + 206.6 TiempoParada + 0.124 PresBarraCal + 0.594 TempMat - 0.00426 TempBarraCal*TempBarraCal - 39.6 TiempoParada*TiempoParada - 0.000532 PresBarraCal*PresBarraCal - 0.00288 TempMat*TempMat - 0.930 TempBarraCal*TiempoParada - 0.000070 TempBarraCal*PresBarraCal - 0.00028 TempBarraCal*TempMat + 0.0440 TiempoParada*PresBarraCal + 0.047 TiempoParada*TempMat - 0.00010 PresBarraCal*TempMat |
|---|
Ajustes y diagnósticos para observaciones poco comunes
| Obs | Resistencia | Ajuste | Resid | Resid est. | |
|---|---|---|---|---|---|
| 3 | 20.69 | 14.43 | 6.26 | 2.20 | R |
| 5 | 27.43 | 21.72 | 5.71 | 2.01 | R |
| 9 | 25.99 | 20.16 | 5.83 | 2.05 | R |
| 19 | 21.38 | 15.10 | 6.28 | 2.21 | R |