Crear un experimento con 2 o más factores continuos

Detalles de la decisión

La siguiente información define los efectos principales, los efectos de interacción, un factor difícil de cambiar y los efectos cuadráticos.

¿Cuál es el efecto principal?

Un efecto principal es una estimación del efecto de un solo factor. Por ejemplo, la empresa de fertilizantes B compara la tasa de crecimiento de las plantas en plantas tratadas con su producto en comparación con plantas tratadas con el fertilizante de la empresa A. En el experimento, el fertilizante B tiene una tasa media de crecimiento de plantas más alta que el fertilizante A. La diferencia en las medias es el principal efecto del factor fertilizante.

¿Qué es un efecto de interacción?

Un efecto de interacción es una estimación de la forma en que el efecto de un factor depende del valor de uno o más factores. Por ejemplo, si los niveles son lo suficientemente amplios, el efecto del tiempo en la calidad de un producto horneado depende de la temperatura. Cuando la temperatura es tan baja que el producto está poco cocido, entonces un aumento en el tiempo aumenta la calidad. Cuando la temperatura está en un rango aceptable, un aumento en el tiempo disminuye la calidad porque el producto se quema. El efecto del tiempo depende del valor de la temperatura.

¿Qué es un factor difícil de cambiar?

Un factor difícil de cambiar es un factor que es difícil de aleatorizar completamente debido a limitaciones de tiempo o costo. Por ejemplo, la temperatura es un factor difícil de cambiar común, porque al ajustar la temperatura, por lo general se requiere un tiempo significativo para que se estabilice. Un diseño de parcela dividida es un experimento diseñado que incluye al menos un factor difícil de cambiar. En un experimento de parcelas divididas, los niveles del factor difícil de cambiar se mantienen constantes durante varias ejecuciones experimentales.

¿Qué son los efectos cuadráticos?

Un efecto cuadrático es un término que permite que el efecto de un factor continuo sobre la respuesta cambie dependiendo del nivel del factor. Por ejemplo, si los niveles son lo suficientemente amplios, el efecto de la temperatura en la calidad de un producto horneado es cuadrático. Cuando la temperatura es tan baja que el producto está poco cocido, un aumento de la temperatura aumenta la calidad. Cuando la temperatura está en un rango aceptable, un aumento de temperatura disminuye la calidad porque el producto se quema. El efecto de la temperatura depende del valor de la temperatura.

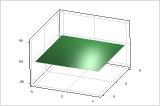
Superficie de respuesta sin efectos cuadráticos

Superficie de respuesta con efectos cuadráticos

Para recopilar datos de la manera más eficiente posible, muchos experimentos incluyen solo 2 niveles de factores continuos, aunque son muchos más valores posibles. Con solo 2 niveles, los efectos cuadráticos son imposibles de estimar. Normalmente, se estiman los efectos cuadráticos en un experimento porque se tiene conocimiento del proceso de que el efecto existe o porque las ejecuciones experimentales anteriores muestran que el efecto existe. En los experimentos diseñados, normalmente se seleccionan los factores importantes y se utiliza un pequeño número de puntos centrales para comprobar la curvatura antes de realizar un experimento que calcule los efectos cuadráticos. La recopilación de datos para estimar los efectos cuadráticos cuando no hay efectos cuadráticos aumenta el costo del experimento sin proporcionar más información.

Siguiente

• Estimación de los efectos principales y de interacción: Crear diseño factorial de 2 niveles.
• Estimar los efectos principales y de interacción cuando algunos factores son difíciles de cambiar: Crear diseño de parcela dividida de 2 niveles.
• Estimación de los efectos principales, de interacción y cuadráticos: Crear diseño de superficie de respuesta.