Métodos y fórmulas para los ajustes y residuos en Analizar diseño de mezcla

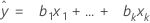
Los diseños de mezcla no incluyen una constante.

Notación

Término	Description
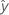	valor ajustado
xk	késimo término. Cada término puede ser un solo predictor, un término polinómico o un término de interacción.
bk	estimación del késimo coeficiente de regresión

El error estándar del valor ajustado en un modelo de regresión con un predictor es:

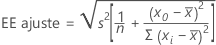
El error estándar del valor ajustado en un modelo de regresión con más de un predictor es:

Notación

Término	Description
s2	cuadrado medio del error
n	número de observaciones
x0	nuevo valor del predictor
	media del predictor
xi	iésimo valor predictor
x0	vector de valores que produce los valores ajustados, uno para cada columna en la matriz de diseño
x'0	transpuesta del nuevo vector de valores predictores
X	matriz de diseño

El residuo es la diferencia entre un valor observado y el valor ajustado correspondiente. Esta parte de la observación no es explicada por el modelo. El residuo de una observación es:

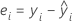
Notación

Término	Description
yi	valor de la iésima respuesta observada
	iésimo valor ajustado para la respuesta

Los residuos estandarizados también se denominan residuos "studentizados internamente".

Fórmula

Notación

Término	Description
ei	i ésimo residuo
hi	i ésimo elemento diagonal de X(X'X)–1X'
s2	cuadrado medio del error
X	matriz de diseño
X'	transpuesta de la matriz de diseño

También conocidos como residuos studentizados externamente. La fórmula es:

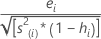
Otra presentación de esta fórmula es:

El modelo que estima la i^ésima observación, omite la i^ésimaobservación del conjunto de datos. Por lo tanto, la i^ésima observación no puede influir en la estimación. Cada residuo eliminado tiene una distribución t de Student con 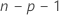grados de libertad.

Notación

Término	Description
ei	iésimo residuo
s(i)2	cuadrado medio del error calculado sin la iésima observación
hi	iésimo elemento diagonal de X(X'X)–1X'
n	número de observaciones
p	número de términos
SSE	suma de los cuadrados para el error