En este tema
Apalancamientos (Hi)
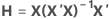
El apalancamiento de la iésima observación es el iésimo elemento diagonal, hi de H. Si hi es grande, la iésima observación tiene predictores poco comunes (X1i, X2i, ..., Xpi). Es decir, los valores predictores están lejos del vector medio (X1, X2,..., Xp), utilizando la distancia de Mahalanobis.
Los valores de apalancamiento están entre 0 y 1. Minitab identifica las observaciones con apalancamientos superiores a 3p/n o .99, el valor que sea menor, con una X en la tabla de observaciones poco comunes. Por lo general, los valores con apalancamientos grandes se examinan.
Notación
| Término | Description |
|---|---|
| X | matriz de diseño |
| hi | iésimo elemento diagonal de la matriz hat |
| p | número de términos en el modelo |
| n | número de observaciones |
Distancia de Cook
La medida general, D, del impacto combinado de todos los coeficientes de regresión estimados sobre una observación. Minitab calcula D utilizando los valores de apalancamiento y los residuos estandarizados, y considera si una observación es poco común con respecto a los valores de X y los valores de Y. Las observaciones con valores D grandes pueden ser valores atípicos.
Fórmula
La distancia de Cook es la distancia entre los coeficientes calculados con y sin la iésima observación. Minitab calcula la distancia de Cook sin ajustar una nueva ecuación de regresión cada vez que se omite una observación. Este cálculo es:

Notación
| Término | Description |
|---|---|
| ei | iésimo residuo |
| hi | iésimo elemento diagonal de 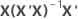 |
| p | número de parámetros del modelo |
| s2 | cuadrado medio del error |
| b | vector de coeficientes |
| b(i) | vector de coeficientes calculado después de eliminar la iésima observación |
| X | matriz de diseño |
DFITS
Combina los valores de apalancamiento y de residuos studentizados (residuos t eliminados) en una medida general de qué tan poco común es una observación. DFITS mide la influencia de cada observación en los valores ajustados de un modelo de regresión y ANOVA. Las observaciones con valores grandes de DFITS podrían ser valores atípicos.
DFITS representa aproximadamente el número de desviaciones estándar que el valor ajustado cambia cuando cada observación es eliminada del conjunto de datos y se vuelve a ajustar el modelo. Minitab puede calcular DFITS sin ajustar una nueva ecuación de regresión cada vez que se omite una observación.
Fórmula

Notación
| Término | Description |
|---|---|
| ei | iésimo residuo |
| hi | iésimo elemento diagonal de 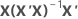 |
| X | matriz de diseño |
 | iésima respuesta ajustada |
 | valor ajustado calculado sin la iésima observación |
| MSE (i) | cuadrado medio del error calculado sin la iésima observación |
| n | número de observaciones |
| p | número de parámetros del modelo |
