En este tema
Coeficiente (Coef)
Minitab utiliza la estimación de los mínimos cuadrados para calcular los coeficientes.
En términos de matriz, las estimaciones de los mínimos cuadrados de los coeficientes son:
b = (X'X)-1X'y
Para obtener más información sobre los coeficientes de los modelos de orden superior, consulte a Cornell1.
Notación
| Término | Description |
|---|---|
| X | matriz de diseño |
| y | columna de respuestas |
- J.A. Cornell (1990). Experiments With Mixtures: Designs, Models, and the Analysis of Mixture Data, John Wiley & Sons.
Error estándar del coeficiente (EE Coef)
Para la regresión lineal simple, el error estándar del coeficiente es:
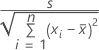
Los errores estándar de los coeficientes para la regresión múltiple son las raíces cuadradas de los elementos diagonales de esta matriz:
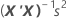
Notación
| Término | Description |
|---|---|
| xi | iésimo valor predictor |
 | media del predictor |
| X | matriz de diseño |
| X' | transposición de la matriz de diseño |
| s2 | cuadrado medio del error |
Valor t
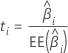
Notación
| Término | Description |
|---|---|
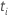 | estadístico de prueba para el  coeficiente coeficiente |
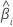 |  coeficiente estimado coeficiente estimado |
 | error estándar del  coeficiente estimado coeficiente estimado |
Valor p – Tabla Coeficientes
El valor p bilateral para la hipótesis nula de que un coeficiente de regresión es igual a 0 es:
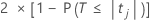
Los grados de libertad son los grados de libertad para el error, como se indica a continuación:
n – p
Notación
| Término | Description |
|---|---|
 | La función de distribución acumulada de la distribución t con grados de libertad iguales a los grados de libertad para el error. |
| tj | El estadístico t para el jésimo coeficiente. |
| n | El número de observaciones en el conjunto de datos. |
| p | La suma de los grados de libertad para los términos. |
Factor de inflación de la varianza (FIV)
El FIV se puede obtener haciendo la regresión de cada predictor sobre los predictores restantes y registrando el valor de R2.
Fórmula
Para el predictor xj, el FIV es:

Notación
| Término | Description |
|---|---|
| R2(xj) | el coeficiente de determinación con xj como la variable de respuesta y los otros términos del modelo como los predictores |
