En este tema
Ajuste
Los valores ajustados también se denominan ajustes o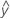 
. Los valores ajustados son estimados de puntos de la respuesta media para los valores dados de los predictores. Los valores de los predictores también se denominan valores x.
Interpretación
Los valores ajustados se calculan ingresando los valores específicos de X para cada observación del conjunto de datos en la ecuación del modelo.
Por ejemplo, si la ecuación es y = 5 + 10x, el valor ajustado para el valor x, 2, es 25 (25 = 5 + 10(2)).
Las observaciones con valores ajustados que sean muy diferentes del valor observado pueden ser poco comunes. Las observaciones con valores predictores poco comunes podrían ser influyentes. Si Minitab determina que los datos incluyen valores poco comunes o influyentes, la salida incluye la tabla Ajustes y diagnósticos para observaciones poco comunes, que identifica estas observaciones. Las observaciones poco comunes que Minitab etiqueta no siguen adecuadamente la ecuación de regresión propuesta. Sin embargo, se espera que haya algunas observaciones poco comunes. Por ejemplo, con base en los criterios para los residuos estandarizados grandes, se esperaría que aproximadamente el 5% de las observaciones se marque como observaciones que tienen un residuo estandarizado grande. Para obtener más información sobre valores poco comunes, vaya a Observaciones poco comunes.
EE ajuste
El error estándar del ajuste (EE ajuste) estima la variación en la respuesta media estimada para la configuración especificada de las variables. El cálculo del intervalo de confianza para la respuesta media utiliza el error estándar del ajuste. Los errores estándar siempre son no negativos.
Interpretación
Utilice el error estándar del ajuste para medir la precisión de la estimación de la respuesta media. Cuanto menor sea el error estándar, más precisa será la respuesta media pronosticada. Por ejemplo, un analista desarrolla un modelo para pronosticar el tiempo de entrega. Para un conjunto de valores de configuración de las variables, el modelo predice un tiempo medio de entrega de 3.80 días. El error estándar del ajuste para estos valores de configuración es 0.08 días. Para un segundo conjunto de valores de configuración de las variables, el modelo produce el mismo tiempo medio de entrega con un error estándar del ajuste de 0.02 días. El analista puede estar más seguro de que el tiempo medio de entrega del segundo conjunto de valores de configuración de las variables está cerca de 3.80 días.
Con el valor ajustado, usted puede utilizar el error estándar del ajuste para crear un intervalo de confianza para la respuesta media. Por ejemplo, dependiendo del número de grados de libertad, un intervalo de confianza de 95% se extiende aproximadamente dos errores estándar por encima y por debajo de la media pronosticada. Para los tiempos de entrega, el intervalo de confianza de 95% de la media pronosticada de 3.80 días cuando el error estándar es 0.08 es (3.64, 3.96) días. Usted puede estar 95% seguro de que la media de la población se encuentra dentro de este rango. Cuando el error estándar es 0.02, el intervalo de confianza de 95% es (3.76, 3.84) días. El intervalo de confianza del segundo conjunto de valores de configuración de las variables es más estrecho porque el error estándar es menor.
Residuos
Un residuo (ei) es la diferencia entre un valor observado (y) y el valor ajustado correspondiente, (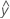
), el cual es el valor pronosticado por el modelo.
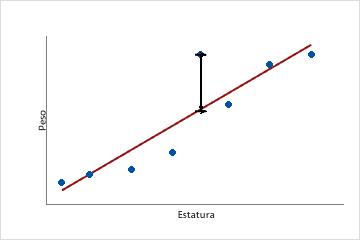
Esta gráfica de dispersión muestra el peso vs. la estatura para una muestra de adultos hombres. La línea de regresión ajustada representa la relación entre estatura y peso. Si la estatura equivale a 6 pies, el valor ajustado para el peso es de 190 libras. Si el peso real es de 200 libras, el residuo es de 10.
Interpretación
Método que se utiliza cuando se viola el supuesto de cuadrados mínimos de la varianza constante en los residuos (heteroscedasticidad). Graficar los residuos para determinar si el modelo es adecuado y cumple con los supuestos de regresión. Examinar los residuos puede ofrecer información útil de hasta qué punto el modelo se ajusta a los datos. En general, los residuos deben ser distribuidos aleatoriamente sin patrones evidentes y sin valores poco comunes. Si Minitab determina que los datos incluyen observaciones poco comunes, identifica esas observaciones en la tabla Ajustes y diagnósticos para observaciones poco comunes en el resultado. Las observaciones que Minitab etiqueta como poco comunes no siguen adecuadamente la ecuación de regresión propuesta. Sin embargo, se espera que se tengan algunas observaciones poco comunes. Por ejemplo, con base en los criterios para los residuos grandes, se esperaría que aproximadamente el 5 % de las observaciones sean etiquetadas como con un residuo grande. Para obtener más información sobre valores poco comunes, vaya a Observaciones poco comunes.
Residuo estandarizado
El residuo estandarizado es igual al valor de un residuo (ei) dividido entre una estimación de su desviación estándar.
Interpretación
Utilice los residuos estandarizados como ayuda para detectar valores atípicos. Los residuos estandarizados mayores que 2 y menores que −2 por lo general se consideran grandes. La tabla Ajustes y diagnósticos para observaciones inusuales identifica estas observaciones con una 'R'. Las observaciones que Minitab etiqueta no siguen adecuadamente la ecuación de regresión propuesta. Sin embargo, se espera que se tengan algunas observaciones poco comunes. Por ejemplo, con base en los criterios para los residuos estandarizados grandes, se esperaría que aproximadamente el 5% de las observaciones se etiquete como con un residuo estandarizado grande. Para obtener más información, vaya a Observaciones poco comunes.
Los residuos estandarizados son útiles porque los residuos sin procesar podrían no ser buenos indicadores de valores atípicos. La varianza de cada residuo sin procesar puede diferir por los valores x asociados con la misma. Esta variación desigual hace que sea dificil evaluar las magnitudes de los residuos sin procesar. Al estandarizar los residuos se resuelve el problema conviertiendo las diferentes varianzas en una escala común.
