En este tema
Método
Minitab utiliza dos métodos para analizar las desviaciones estándar de las mediciones de repeticiones o réplicas: mínimos cuadrados y máxima verosimilitud. Ambos métodos se basan en un modelo lineal con una función de enlace de logaritmo: ln(σ) = Aγ, donde A es la matriz de diseño e y es un vector de parámetros que se estimarán. Una ventaja de utilizar la función de enlace de logaritmo es que los valores ajustados son siempre positivos.
Los dos métodos producen resultados equivalentes en el modelo saturado, cuando el número de parámetros es igual al número de puntos de datos.
Para la estimación de mínimos cuadrados, Minitab utiliza regresión de mínimos cuadrados ponderada. Si el número de repeticiones o réplicas es igual, las ponderaciones son iguales.
Para MLE, Minitab presupone que los datos originales provienen de una distribución normal. La distribución de la varianza de la muestra se relaciona con la distribución χ2.
Matriz de diseño
Minitab utiliza el mismo enfoque para la matriz de diseño que el usado en el modelo lineal general (GLM), el cual utiliza regresión para ajustar el modelo que usted especifique. Primero Minitab crea una matriz de diseño a partir de los factores y el modelo que se especifique. Las columnas de esta matriz, denominada X, representa los términos en el modelo.
La matriz de diseño tiene n filas, donde n = número de observaciones y varios bloques de columnas correspondientes a los términos en el modelo. El primer bloque se reserva para la constante y contiene solo una columna formada por números uno. El bloque de un factor continuo también contiene solo una columna. El bloque de columnas de un factor categórico contiene r columnas, donde r = grados de libertad del factor.
Por ejemplo, un diseño factorial fraccionado tiene tres factores con 2 niveles cada uno. El modelo incluye 3 efectos principales. Cada fila tiene uno de los siguientes códigos:
| Bloques | Factor 1 | Factor 2 | Factor 3 |
|---|---|---|---|
| 1 | −1 | −1 | −1 |
| 1 | 1 | −1 | −1 |
| 1 | −1 | 1 | −1 |
| 1 | 1 | 1 | −1 |
| 1 | −1 | −1 | 1 |
| 1 | 1 | −1 | 1 |
| 1 | −1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
Efectos
Los efectos estimados de cada factor. Los efectos solo se calculan para modelos de dos niveles y no se calculan para modelos factoriales generales. La fórmula para el efecto de un factor es:
Efecto = Coeficiente * 2
Coeficientes (Coef.)
Las estimaciones de los coeficientes de regresión de la población en una ecuación de regresión. Para cada coeficiente, Minitab calcula k - 1 coeficientes, donde k es el número de niveles en el factor. Para un modelo factorial completo de 2 niveles y 2 factores, las fórmulas para coeficientes de los factores y las interacciones son:


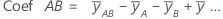
El error estándar del coeficiente para este modelo factorial completo de 2 niveles y 2 factores es:

Para obtener información sobre modelos con más de dos factores o factores con más de dos niveles, véase Montgomery1.
Notación
| Término | Description |
|---|---|
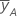 | media de y en el nivel alto del factor A |
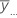 | media general de todas las observaciones |
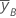 | media de y en el nivel alto del factor B |
 | media de y en los niveles altos de A y B |
| MSE | cuadrado medio del error |
| n | número de - 1 y 1 (en la matriz de covarianzas) para el término estimado |
Regresión ponderada
La regresión de mínimos cuadrados ponderados es un método para tratar las observaciones que tienen varianzas no constantes. Si las varianzas no son constantes, a las observaciones con:
- grandes varianzas se les debe ofrecer ponderaciones relativamente pequeñas
- pequeñas varianzas se les debe ofrecer ponderaciones relativamente grandes
Las ponderaciones reflejan el número de repeticiones o réplicas utilizadas para calcular cada desviación estándar. Las desviaciones estándar basadas en más datos reciben ponderaciones más grandes.
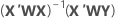
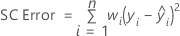
Notación
| Término | Description |
|---|---|
| X | matriz de diseño |
| X' | transpuesta de la matriz de diseño |
| W | una matriz n x n con las ponderaciones en la diagonal |
| Y | vector de valores de desviaciones estándar logarítmicas |
| n | número de observaciones |
| wi | ponderación de la iésima observación |
| yi | valor de la desviación estándar logarítmica de la iésima observación |
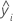 | valor ajustado de la desviación estándar logarítmica de la iésima observación |
Cálculo de ponderaciones
Usted puede calcular y almacenar ponderaciones utilizando varianzas ajustadas con base en el modelo de dispersión que se usará al analizar el modelo de ubicación.
- 1 / varianza ajustada
- σ2(subgrupos) + σ2 (corto plazo) / número de repeticiones
"Subgrupos" y "corto plazo" se refieren a una corrida del experimento. La variación dentro de una corrida es lo que usted mide con las desviación estándar de observaciones repetidas. La variación entre corridas se refiere a las fuentes adicionales de variación por causa de nuevas corridas.
Cuando usted analiza la desviación estándar en las repeticiones, ajusta un modelo a s (corto plazo). Si tiene réplicas, Minitab combina el modelo para σ2 (corto plazo) y la varianza de medias entre réplicas para obtener una estimación de σ2 (subgrupos). Luego, la estimación de σ2 (subgrupos) se recombina con σ2 (corto plazo) / número de repeticiones para obtener estimaciones de varianza para las medias que concuerden con el modelo de dispersión.
Este enfoque presupone que σ2(subgrupos) es constante y no depende de los niveles de los factores. Si este supuesto es incorrecto, se recomienda que ajuste un modelo a la varianza de x utilizando Respuestas antes del proceso con  para obtener σ2 en las réplicas.
para obtener σ2 en las réplicas.
Si tiene covariables en su modelo, debe representarlas en la varianza de las repeticiones. No puede representar covariables en la varianza ajustada.
