Matriz de diseño
Minitab utiliza el mismo enfoque para la matriz de diseño que el usado en el modelo lineal general (GLM), el cual utiliza regresión para ajustar el modelo que usted especifique. Primero Minitab crea una matriz de diseño a partir de los factores y el modelo que se especifique. Las columnas de esta matriz, denominada X, representa los términos en el modelo.
- Constante
- Covariables
- Bloques
- Factores
- Interacciones
- Constante
- Covariable
- Factor continuo
Para los bloques, el número de columnas es uno menos el número de bloques.
Factores categóricos e interacciones en diseños de 2 niveles
En un diseño de 2 niveles, el término de un factor categórico tiene 1 columna. Cualquier término de interacción también tiene 1 columna.
Factores categóricos en diseños factoriales generales
| Nivel de A | A1 | A2 | A3 |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 |
| 4 | -1 | -1 | -1 |
Interacciones en diseños factoriales generales
Para calcular las columnas de un término de interacción, multiplique las columnas correspondientes por los factores en la interacción. Por ejemplo, supongamos que el factor A tiene 6 niveles, C tiene 3 niveles, D tiene 4 niveles. Entonces el término A * C * D tiene 5 x 2 x 3 = 30 columnas. Para obtener los niveles, multiplique cada columna de A por cada una de C, por cada una de D.
Columnas de parcela completa en diseños de parcela dividida
Nota
Minitab no analiza diseños de parcela dividida con una respuesta binaria.
Para un diseño de parcela dividida, Minitab utiliza 2 versiones de la matriz de diseño. Una versión es la misma matriz utilizada para cualquier diseño factorial de 2 niveles. La otra matriz incluye un bloque de columnas que representan parcelas completas. El cálculo, por ejemplo, del término de error de parcela completa utiliza esta segunda versión de la matriz de diseño. Las columnas de parcelas completas siguen las columnas de los factores difíciles de cambiar y las interacciones que involucran solo factores difíciles de cambiar.
Efectos
Los efectos estimados de cada factor. Los efectos solo se calculan para modelos de dos niveles y no se calculan para modelos factoriales generales. La fórmula para el efecto de un factor es:
Efecto = Coeficiente * 2
Coeficientes (Coef.)
Las estimaciones de los coeficientes de regresión de la población en una ecuación de regresión. Para cada coeficiente, Minitab calcula k - 1 coeficientes, donde k es el número de niveles en el factor. Para un modelo factorial completo de 2 niveles y 2 factores, las fórmulas para coeficientes de los factores y las interacciones son:


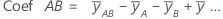
El error estándar del coeficiente para este modelo factorial completo de 2 niveles y 2 factores es:

Para obtener información sobre modelos con más de dos factores o factores con más de dos niveles, véase Montgomery1.
Notación
| Término | Description |
|---|---|
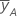 | media de y en el nivel alto del factor A |
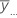 | media general de todas las observaciones |
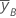 | media de y en el nivel alto del factor B |
 | media de y en los niveles altos de A y B |
| MSE | cuadrado medio del error |
| n | número de - 1 y 1 (en la matriz de covarianzas) para el término estimado |
Transformación de Box-Cox
La transformación de Box Cox selecciona los valores de lambda, como se muestra a continuación, que minimizan la suma de los cuadrados de los residuos. La transformación resultante es Y λ cuando λ ≠ 0 y ln(Y) cuando λ = 0. Cuando λ < 0, Minitab también multiplica la respuesta transformada por −1 para mantener el orden de la respuesta no transformada.
Minitab busca un valor óptimo entre −2 y 2. Los valores que estén fuera de este intervalo podrían no producir un mejor ajuste.
Las siguientes son algunas transformaciones comunes donde Y′ es la transformación de los datos Y:
| Valor de lambda (λ) | Transformación |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0.5 | Y′ = 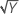 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0.5 |  |
| λ = −1 | Y′ = −1 / Y |
Regresión ponderada
La regresión de mínimos cuadrados ponderados es un método para tratar las observaciones que tienen varianzas no constantes. Si las varianzas no son constantes, a las observaciones con:
- a las grandes varianzas se les debe ofrecer ponderaciones relativamente pequeñas
- a las pequeñas varianzas se les debe ofrecer ponderaciones relativamente grandes
La elección de ponderaciones generalmente es la inversa de la varianza de error puro en la respuesta.
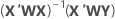
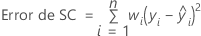
Notación
| Término | Description |
|---|---|
| X | matriz de diseño |
| X' | transpuesta de la matriz de diseño |
| W | una matriz n x n con las ponderaciones en la diagonal |
| Y | vector de valores de respuesta |
| n | número de observaciones |
| wi | ponderación de la iésima observación |
| yi | valor de respuesta de la iésima observación |
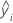 | valor ajustado de la iésima observación |
