Métodos y fórmulas para el análisis de varianza en Analizar diseño factorial

La suma de distancias cuadradas. Las fórmulas presentadas son para un modelo factorial completo de dos factores con factores A y B. Estas fórmulas se pueden extender a modelos con más de dos factores. Para obtener más información, véase Montgomery¹.

La SC total es la variación total en el modelo. SC (A) y SC (B) son la suma de las desviaciones cuadradas de las medias de niveles de factores estimadas alrededor de la media general. El error de SC es la suma de los residuos cuadráticos. Esto se conoce también como un error en los tratamientos. Los cálculos son:

Si el modelo incluye réplicas, SC de Error puro es:

Para casos diferentes del modelo factorial completo de dos factores, usted puede tener otras sumas de cuadrados. Si ajusta un modelo reducido, Falta de ajuste de SC es:

Si el modelo incluye los puntos centrales, Curvatura de SC es:

En diseños de parcela dividida, las sumas de cuadrados para variación de parcela completa y de error para parcela subdividida son:

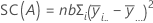
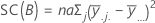
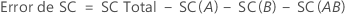
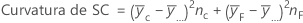
1. D.C. Montgomery (1991). Design and Analysis of Experiments, Third Edition, John Wiley & Sons.

Notación

Término	Description
a	número de niveles en el factor A
b	número de niveles en el factor B
n	número total de réplicas
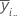	media del iésimo nivel del factor A
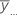	media general de todas las observaciones
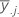	media del jésimo nivel del factor B
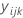	observación en el iésimo nivel del factor A, jésimo nivel del factor B y la késima réplica
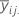	media del iésimo nivel del factor A y el jésimo nivel del factor B
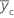	respuesta media de puntos centrales
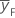	respuesta media para puntos factoriales
nF	número de puntos factoriales

Minitab desglosa el componente SC Regresión o Tratamientos de la varianza en las sumas secuenciales de los cuadrados para cada factor. Las sumas secuenciales de los cuadrados dependen del orden en que los factores o predictores se ingresan en el modelo. Las sumas secuenciales de cuadrados es la porción única de la SC Regresión explicada por un factor, dados los factores ingresados previamente.

Por ejemplo, si se tiene un modelo con tres factores o predictores, X1, X2 y X3, la suma secuencial de cuadrados para X2 muestra qué proporción de la variación restante puede explicar X2, dado que X1 ya se encuentra en el modelo. Para obtener una secuencia diferente de factores, repita el análisis e ingrese los factores en un orden diferente.

Las sumas ajustadas de los cuadrados no dependen del orden en que los términos se ingresan en el modelo. La suma ajustada de los cuadrados es la cantidad de variación explicada por un término, dados todos los otros términos estén incluidos en el modelo, independientemente del orden en que se ingresen los términos en el modelo.

Por ejemplo, si usted tiene un modelo con tres factores, X1, X2 y X3, la suma ajustada de los cuadrados para X2 muestra la proporción de la variación restante que es explicada por el término para X2, dado que los términos para X1 y X3 también se encuentren en el modelo.

Los cálculos de las sumas ajustadas de los cuadrados para tres factores son:

• SSR(X3 | X1, X2) = SSE (X1, X2) - SSE (X1, X2, X3) o
• SSR(X3 | X1, X2) = SSR (X1, X2, X3) - SSR (X1, X2)

donde SSR(X3 | X1, X2) es la suma ajustada de los cuadrados para X3, dado que X1 y X2 estén en el modelo.

• SSR(X2, X3 | X1) = SSE (X1) - SSE (X1, X2, X3) o
• SSR(X2, X3 | X1) = SSR (X1, X2, X3) - SSR (X1)

donde SSR(X2, X3 | X1) es la suma ajustada de los cuadrados para X2 y X3, dado que X1 esté en el modelo.

Usted puede ampliar estas fórmulas si tienen más de 3 factores en el modelo¹.

1. J. Neter, W. Wasserman y M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.

Para un diseño factorial completo con factores A y B y una variable de bloqueo, el número de grados de libertad asociado con cada suma de cuadrados es:

Para interacciones entre factores, multiplique los grados de libertad de los términos en los factores. Por ejemplo, si los factores son A y B, entonces la interacción AB tiene estos grados de libertad:

Para hallar los grados de libertad de un tipo de término, sume los grados de libertad de los términos. Por ejemplo, si los factores son A y B, entonces los efectos principales en el modelo tienen esta cantidad de grados de libertad:

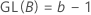
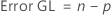
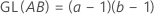
Para diseños de 2 niveles con puntos centrales, el número de grados de libertad para la curvatura es 1.

Una prueba para determinar si los efectos principales y de interacción son significativos. La fórmula para los términos del modelo es:

Los grados de libertad para la prueba son:

• Numerador = grados de libertad para el término
• Denominador = grados de libertad para el error

Valores más grandes de F apoyan rechazar la hipótesis nula de que no hay un efecto significativo.

Para diseños balanceados de parcelas divididas, el estadístico F para factores difíciles de cambiar utiliza los CM para el error de parcela completa en el denominador. Para otros diseños de parcelas divididas, Minitab usa una combinación lineal del Error de PC y el Error de PD para construir un denominador que se base en los cuadrados medios esperados.