Gráficas de efectos para Analizar diseño factorial

Encuentre definiciones y ayuda para interpretar cada gráfica de efectos.

En este tema

Diagrama de Pareto
Gráfica normal de los efectos
Gráfica de normales absolutos de los efectos

Diagrama de Pareto

El diagrama de Pareto muestra los valores absolutos de los efectos estandarizados desde el efecto más grande hasta el efecto más pequeño. Los efectos estandarizados son estadísticos t que prueban la hipótesis nula de que el efecto es 0. El diagrama también muestra una línea de referencia para indicar cuáles efectos son estadísticamente significativos.

La línea de referencia para determinar la significancia estadística depende del nivel de significancia (denotado por α o alfa). A menos que usted utilice un método de selección escalonado que defina un valor alfa, el nivel de significancia es 1 menos el nivel de confianza del análisis. Para obtener más información sobre cómo cambiar el nivel de confianza, vaya a Especificar las opciones para Analizar diseño factorial. Si usa selección hacia atrás o selección escalonada, el nivel de significancia es el nivel de significancia en el que Minitab elimina un término del modelo, conocido como Alfa para retirar. Si usa selección hacia adelante, el nivel de significancia es el nivel de significancia en el que Minitab agrega un término al modelo, conocido como Alfa para ingresar.

Nota

Para un diseño de 2 niveles, si el número de términos incluidos en el modelo es igual al número de corridas, no se pueden calcular los efectos estandarizados. Minitab muestra los efectos no estandarizados y utiliza el método de Lenth para dibujar una línea de referencia para la significancia estadística. Para obtener más información sobre el método de Lenth, vaya a Métodos y fórmulas para las gráficas de efectos en Analizar diseño factorial y haga clic en "Pseudo error estándar de Lenth (PSE)".
Para un diseño factorial completo general, si el número de términos incluidos en el modelo es igual al número de corridas, no se pueden calcular los efectos estandarizados. Minitab no genera un diagrama de Pareto en este caso.

Interpretación

Utilice el diagrama de Pareto para determinar la magnitud y la importancia de los efectos. En el diagrama de Pareto, las barras que cruzan la línea de referencia son estadísticamente significativas. Por ejemplo, en este diagrama de Pareto, las barras que representan los factores C, B y BC cruzan la línea de referencia que está en 2,31. Estos factores son estadísticamente significativos en el nivel de 0,05 con los términos actuales del modelo.

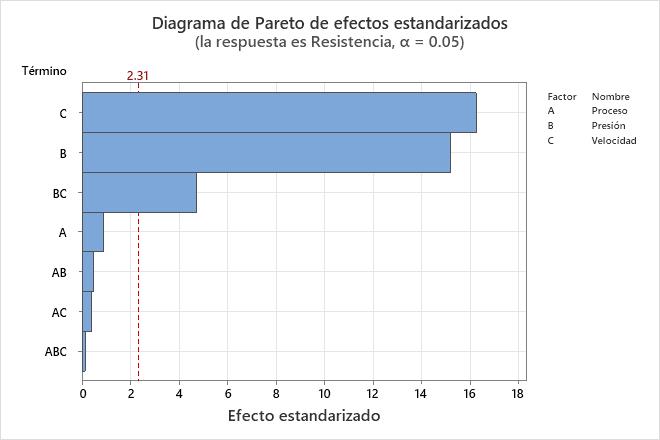
Puesto que el diagrama de Pareto muestra el valor absoluto de los efectos, usted puede determinar cuáles efectos son grandes, pero no puede determinar cuáles efectos aumentan o disminuyen la respuesta. Utilice la gráfica de probabilidad normal de los efectos estandarizados para examinar la magnitud y dirección de los efectos en una gráfica.

Gráfica normal de los efectos

La gráfica de probabilidad normal de los efectos muestra los efectos estandarizados en relación con una línea de ajuste de distribución para el caso en que todos los efectos son 0. Los efectos estandarizados son estadísticos t que prueban la hipótesis nula de que el efecto es 0. Los efectos positivos principales aumentan la respuesta cuando la configuración cambia del valor bajo de un factor al valor alto. Los efectos principales negativos reducen la respuesta cuando la configuración cambia del valor bajo de un factor al valor alto. Los efectos más distantes de 0 en el eje X tienen mayor magnitud. Los efectos más distantes de 0 son estadísticamente más significativos.

Que un efecto sea estadísticamente significativo depende del nivel de significancia (denotado como α o alfa). A menos que usted utilice un método de selección escalonado que defina un valor alfa, el nivel de significancia es 1 menos el nivel de confianza del análisis. Para obtener más información sobre cómo cambiar el nivel de confianza, vaya a Especificar las opciones para Analizar diseño factorial. Si usa selección hacia atrás o selección escalonada, el nivel de significancia es el nivel de significancia en que Minitab elimina un término del modelo, conocido como Alfa a retirar. Si usa selección hacia adelante, el nivel de significancia es el nivel de significancia en que Minitab agrega un término al modelo, conocido como Alfa a entrar

Nota

Para un diseño de 2 niveles, si el número de términos incluidos en el modelo es igual al número de corridas, no se pueden calcular los efectos estandarizados. Minitab muestra los efectos no estandarizados y utiliza el método de Lenth para calcular la distancia crítica para alcanzar significancia estadística. Para obtener más información sobre el método de Lenth, vaya a Métodos y fórmulas para las gráficas de efectos en Analizar diseño factorial y haga clic en "Pseudo error estándar de Lenth (PSE)".

Interpretación

Utilice la gráfica de probabilidad normal de los efectos para determinar la magnitud, la dirección y la importancia de los efectos. En la gráfica de probabilidad normal de los efectos, los efectos que están más distantes de 0 son estadísticamente significativos. El color y la forma de los puntos difieren entre efectos estadísticamente significativos y efectos estadísticamente insignificantes. Por ejemplo, en esta gráfica, los efectos principales de los factores A, B y C son estadísticamente significativos en el nivel 0.05. Estos puntos tienen un color y forma diferentes en comparación con los puntos de los efectos insignificantes.

Además, la gráfica indica la dirección del efecto. Proceso (A) tiene un efecto estandarizado positivo. Cuando el proceso cambia del nivel bajo al nivel alto del factor, se incrementa la respuesta. Presión (B) y Velocidad (C) tienen efectos estandarizados negativos. Cuando Presión y Velocidad aumentan, la respuesta disminuye.

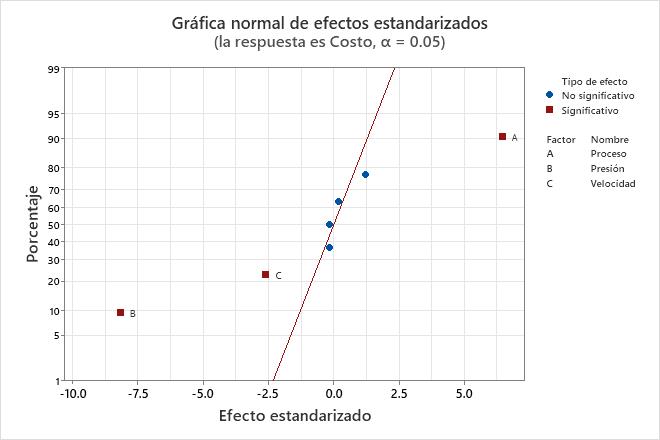
Puesto que la gráfica de probabilidad normal de los efectos muestra los efectos negativos en el lado izquierdo de la gráfica y los efectos positivos en el lado derecho de la gráfica, las comparaciones sobre cuáles efectos cambian en mayor medida la respuesta son más difíciles que en las gráficas que muestran los valores absolutos de los efectos estandarizados. La gráfica de normales absolutos y el diagrama de Pareto muestran los valores absolutos de los efectos estandarizados.

Gráfica de normales absolutos de los efectos

La gráfica de probabilidad de normales absolutos de los efectos muestra los valores absolutos de los efectos estandarizados desde el efecto más grande hasta el efecto más pequeño. Los efectos estandarizados son estadísticos t que prueban la hipótesis nula de que el efecto es 0. Los puntos se muestran en relación con una línea de referencia para el caso en que todos los efectos son 0. Los efectos más alejados de 0 en el eje X tienen mayor magnitud. Los efectos más alejados de 0 son más estadísticamente significativos.

La distancia a la que deben estar los puntos desde la línea de referencia para ser estadísticamente significativos depende del nivel de significancia (denotado por α o alfa). A menos que usted utilice un método de selección escalonado que defina un valor alfa, el nivel de significancia es 1 menos el nivel de confianza del análisis. Para obtener más información sobre cómo cambiar el nivel de confianza, vaya a Especificar las opciones para Analizar diseño factorial. Si usa selección hacia atrás o selección escalonada, el nivel de significancia es el nivel de significancia en que Minitab elimina un término del modelo, conocido como Alfa a retirar. Si usa selección hacia adelante, el nivel de significancia es el nivel de significancia en que Minitab agrega un término al modelo, conocido como Alfa a entrar

Nota

Interpretación

Utilice la gráfica de probabilidad de normales absolutos de los efectos para determinar la magnitud y la importancia de los efectos. En la gráfica de probabilidad de normales absolutos de los efectos, los efectos que están más distantes de 0 son estadísticamente significativos. El color y la forma de los puntos difiere entre efectos estadísticamente significativos y efectos estadísticamente insignificantes. Por ejemplo, en esta gráfica, los efectos principales de los factores A, B y C son estadísticamente significativos en el nivel 0.05. Estos puntos tienen un color y forma diferentes en comparación con los puntos de los efectos insignificantes. Además, Minitab coloca etiquetas en los puntos estadísticamente significativos.

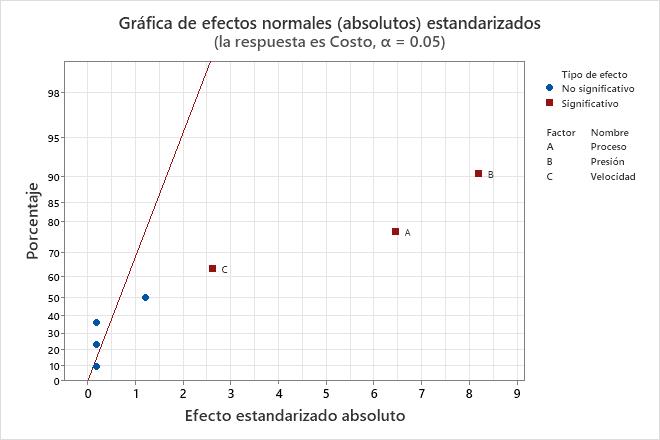
Puesto que la gráfica de probabilidad de normales absolutos de los efectos muestra el valor absoluto de los efectos, usted puede determinar cuáles efectos son grandes, pero no puede determinar cuáles efectos aumentan o disminuyen la respuesta. Utilice la gráfica de probabilidad normal de los efectos estandarizados para ver la magnitud y dirección de los efectos en una gráfica.