Familia exponencial y funciones de enlace
La extensión de los modelos lineales clásicos a modelos lineales generalizados consta de dos partes: una distribución de la familia exponencial y una función de enlace.
La familia exponencial
La primera parte extiende el modelo lineal a las variables de respuesta que son miembros de una familia grande de distribuciones llamada la familia exponencial. Los miembros de la familia exponencial de distribuciones tienen funciones de distribución de probabilidad para una respuesta observada con la siguiente forma general:
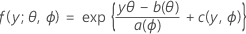
donde a(∙), b(∙) y c(∙) dependen de la distribución de la variable de respuesta. El parámetro θ es un parámetro de ubicación que suele mencionarse como el parámetro canónico y ϕ se denomina parámetro de dispersion. La función a(ϕ) por lo general tiene la forma a(ϕ)= ϕ/ ω, donde ω es una constante conocida o ponderación que puede variar de una observación a otra. (En Minitab, cuando se especifican ponderaciones, la función a(ϕ) se ajusta según corresponda.)
Los miembros de la familia exponencial pueden ser distribuciones discretas o distribuciones continuas. Las distribuciones normal y gamma son ejemplos de distribuciones continuas que son miembros de la familia exponencial. Las distribuciones binomial y de Poisson son ejemplos de distribuciones discretas que son miembros de la familia exponencial. La siguiente tabla contiene las características de algunas de estas distribuciones.
| Distribución | ϕ | b(θ) | a(φ) | c(y, ϕ) |
| Normal | σ2 | θ2/2 | φω |  |
| Binomial | 1 | 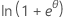 |
φ/ω | -ln(y!) |
| Poisson | 1 | exp(θ) | φ/ω |  |
La función de enlace
La segunda parte es la función de enlace. La función de enlace relaciona la media de la respuesta en la iésima observación con un predictor lineal que tiene esta forma:
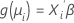
El modelo lineal clásico es un caso especial de esta formulación general donde la función de enlace es la función identidad.
La elección de la función de enlace en la segunda parte depende de la distribución específica de la familia exponencial de la primera parte. En particular, cada distribución de la familia exponencial tiene una función de enlace especial denominada función canónica de enlace. Esta función de enlace satisface la ecuación g (μi) = Xi'β= θ, donde θ es el parémetro canónico. La función canónica de enlace produce ciertas propiedades estadísticas deseables del modelo. Las estadísticas de bondad del ajuste se pueden usar para comparar ajustes utilizando diferentes funciones de enlace. Ciertas funciones de enlace se pueden utilizar por razones históricas o porque tienen un significado especial dentro de una disciplina. Por ejemplo, una ventaja de la función de enlace logit es que proporciona una estimación de las relaciones de probabilidades. Otro ejemplo es que la función de enlace normit presupone que hay una variable subyacente que sigue una distribución normal que se clasifica en categorías binarias.
Minitab ofrece tres funciones de enlace. Las diferentes funciones de enlace permiten encontrar modelos que se ajustan adecuadamente a una variedad más amplia de datos. Las funciones de enlace son logit, normit (también conocida como probit) y gompit (también denominada log-log complementario). Éstas son la inversa de la función de distribución logística acumulada estándar (logit), la inversa de la función de distribución normal acumulada estándar (normit) y la inversa de la función de distribución Gompertz (gompit). El logit es la función canónica de enlace para los modelos binomiales y, por lo tanto, el logit es la función de enlace predeterminada.
| Modelo | Nombre | Función de enlace, g(μi) |
| Binomial | logit | 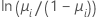 |
| Binomial | normit (probit) | 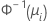 |
| Binomial | gompit (log-log complementario) |  |
Notación
| Término | Description |
|---|---|
| μi | la respuesta media de la iésima fila |
| g(μi) | la función de enlace |
| X | el vector de las variables predictoras |
| β | el vector de los coeficientes asociado con los predictores |
 | la función de distribución acumulada inversa de la distribución normal |
Patrón de factor/covariable
Describe un conjunto individual de valores de factor/covariable en un conjunto de datos. Minitab calcula las probabilidades del evento, los residuos y otras medidas de diagnóstico para cada patrón de factor/covariable.
Por ejemplo, si un conjunto de datos incluye los factores sexo y raza y la covariable edad, la combinación de estos predictores puede contener tantos patrones diferentes de covariables como sujetos. Si un conjunto de datos solamente incluye los factores raza y sexo, cada uno codificado en dos niveles, solo hay cuatro patrones posibles de factor/covariable. Si usted ingresa los datos como frecuencias o como éxitos, ensayos o fracasos, cada fila contiene un patrón de factor/covariable.
Matriz de diseño
Minitab utiliza el mismo enfoque para la matriz de diseño que el usado en el modelo lineal general (GLM), el cual utiliza regresión para ajustar el modelo que usted especifique. Primero Minitab crea una matriz de diseño a partir de los factores y el modelo que se especifique. Las columnas de esta matriz, denominada X, representa los términos en el modelo.
- Constante
- Covariables
- Bloques
- Factores
- Interacciones
- Constante
- Covariable
- Factor continuo
Para los bloques, el número de columnas es uno menos el número de bloques.
Factores categóricos e interacciones en diseños de 2 niveles
En un diseño de 2 niveles, el término de un factor categórico tiene 1 columna. Cualquier término de interacción también tiene 1 columna.
Factores categóricos en diseños factoriales generales
| Nivel de A | A1 | A2 | A3 |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 |
| 4 | -1 | -1 | -1 |
Interacciones en diseños factoriales generales
Para calcular las columnas de un término de interacción, multiplique las columnas correspondientes por los factores en la interacción. Por ejemplo, supongamos que el factor A tiene 6 niveles, C tiene 3 niveles, D tiene 4 niveles. Entonces el término A * C * D tiene 5 x 2 x 3 = 30 columnas. Para obtener los niveles, multiplique cada columna de A por cada una de C, por cada una de D.
Columnas de parcela completa en diseños de parcela dividida
Nota
Minitab no analiza diseños de parcela dividida con una respuesta binaria.
Para un diseño de parcela dividida, Minitab utiliza 2 versiones de la matriz de diseño. Una versión es la misma matriz utilizada para cualquier diseño factorial de 2 niveles. La otra matriz incluye un bloque de columnas que representan parcelas completas. El cálculo, por ejemplo, del término de error de parcela completa utiliza esta segunda versión de la matriz de diseño. Las columnas de parcelas completas siguen las columnas de los factores difíciles de cambiar y las interacciones que involucran solo factores difíciles de cambiar.
