En este tema
Desviación

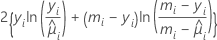
Los grados de libertad para la prueba dependen del tamaño de la muestra y el número de términos incluidos en el modelo:

Notación
| Término | Description |
|---|---|
| Lf | la log-verosimilitud para el modelo completo |
| Lc | la log-verosimilitud del modelo con un subconjunto de términos del modelo completo |
| yi | el número de eventos para la iésima fila de los datos |
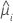 | la respuesta media estimada para la iésima fila de los datos |
| mi | el número de ensayos para la iésima fila de los datos |
| n | el número de filas en los datos |
| p | los grados de libertad para la regresión |
Pearson
El estadístico generalizado de chi-cuadrada de Pearson evalúa la diferencia relativa entre los valores observados y ajustados.
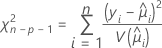
Los grados de libertad para la prueba dependen del tamaño de la muestra y el número de términos incluidos en el modelo. El estadístico de Pearson tiene una distribución de chi-cuadrada exacta para los datos normales. Para los datos no normales, como la distribución binomial y la distribución de Poisson, el estadístico se aproxima a la distribución de forma asintótica.
Notación
| Término | Description |
|---|---|
| n | el número de filas en los datos |
| p | los grados de libertad para la regresión |
| yi | el valor de respuesta para el iésimo patrón de factor/covariable |
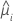 | la respuesta media estimada de la iésima fila |
| V(·) | la función de varianza para el modelo, definida a continuación |
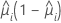
Hosmer-Lemeshow
La fórmula es:
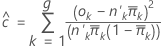
Para formar los grupos, Minitab ordena las probabilidades estimadas y luego intenta crear 10 grupos de igual tamaño.
El número esperado de eventos en un grupo es:
eventos esperados = 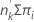
El valor esperado para el número de no eventos es:
no eventos esperados = 
Notación
| Término | Description |
|---|---|
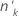 | El número de ensayos en el késimo grupo |
| ok | El número de eventos entre los 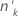 patrones de factores/covariables patrones de factores/covariables |
 | La probabilidad promedio estimada para cada grupo |
| πi | Las probabilidades ajustadas para los patrones de factores/covariables en un grupo |
