Métodos y fórmulas para el análisis de varianza en Analizar respuesta binaria para diseño factorial

La desviación mide la discrepancia entre el modelo actual y el modelo completo. El modelo completo es el modelo que tiene n parámetros, un parámetro por observación. El modelo completo maximiza la función de log-verosimilitud. El modelo completo proporciona un punto de comparación para los modelos con menos de n parámetros. Las comparaciones con el modelo completo utilizan la desviación de escala.

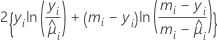
La tabla de desviación se construye con base en el siguiente resultado general que presupone que se conoce el valor de ϕ. Si D_I es la desviación asociada a un modelo inicial y D_S es la desviación asociada a un subconjunto de términos del modelo inicial, entonces, bajo ciertas condiciones de regularidad, existe la siguiente relación:

La diferencia entre las desviaciones se distribuye asintóticamente como una distribución de chi-cuadrada con d grados de libertad. Estos estadísticos se calculan para el análisis ajustado (tipo III) y el análisis secuencial (tipo I). El estadístico de desviación ajustada y el estadístico de chi-cuadrada que contiene la tabla de desviación son iguales. La desviación media ajustada es la desviación ajustada dividida entre los grados de libertad.

Para el análisis secuencial, la salida depende del orden en que los predictores entran al modelo. La desviación secuencial es la única parte de la desviación que es explicada por un predictor, dado que ya haya otros predictores en el modelo. Si usted tiene un modelo con tres predictores, X1, X2 y X3, la desviación secuencial para X3 muestra qué tanto de la desviación restante es explicada por X3 dado que X1 y X2 ya están en el modelo. Para obtener una desviación secuencial diferente, repita el procedimiento de regresión ingresando los predictores en un orden diferente.

Si no se conoce ϕ, para las respuestas que siguen una distribución normal, entonces, bajo ciertas condiciones de regularidad, la relación cambia a lo siguiente:

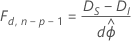
En este caso, la diferencia entre las desviaciones se distribuye asintóticamente como una distribución F con d grados de libertad para el numerador y n − p grados de libertad para el denominador. Para estimar el parámetro de dispersión, utilice el modelo inicial.

Notación

Término	Description
yi	el número de eventos para la iésima fila
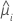	la respuesta media estimada de la iésima fila
mi	el número de ensayos para la iésima fila
Lf	la log-verosimilitud del modelo completo
Lc	la log-verosimilitud del modelo con un subconjunto de términos del modelo completo
d	los grados de libertad son la diferencia entre el número de parámetros de los modelos que se compararán
ϕ	el parámetro de dispersión, que se sabe que es 1 para el modelo binomial
n	el número de filas en los datos
p	los grados de libertad para la regresión en el modelo inicial

Indica el número de informaciones independientes que involucran los datos de respuesta necesarios para calcular las desviaciones medias ajustadas. Los grados de libertad para cada componente del modelo son:

Notación

Término	Description
p	La suma de los grados de libertad para los predictores. Los predictores no incluyen la constante.
n	El número de filas en el diseño
q	El número de niveles del predictor categórico
b	El número de bloques
a	El número de niveles en el factor A
b	El número de niveles en el factor B

Las funciones de log-verosimilitud se parametrizan en términos de las medias. La siguiente es la forma general de las funciones:

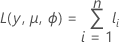
La siguiente es la forma general de las contribuciones individuales:

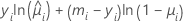
Notación

Término	Description
yi	el número de eventos para la iésima fila
mi	el número de ensayos para la iésima fila
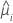	la respuesta media estimada de la iésima fila

Se utilizan en las pruebas de hipótesis como ayuda para decidir si se puede rechazar o no una hipótesis nula. El valor p es la probabilidad de obtener un estadístico de prueba que sea por lo menos tan extremo como el valor real calculado, si la hipótesis nula es verdadera. Un valor de corte que se utiliza comúnmente para el valor p es 0.05. Por ejemplo, si el valor p calculado de un estadístico de prueba es menor que 0.05, usted rechaza la hipótesis nula.