¿Qué es MANOVA (análisis multivariado de la varianza)?
- Aumento en la potencia
- Se puede utilizar la estructura de covarianza de los datos entre las variables de respuesta para probar la igualdad de medias al mismo tiempo. Si las variables de respuesta están correlacionadas, entonces esta información adicional puede ayudar a detectar diferencias muy pequeñas, las cuales no sería posible detectar mediante la ejecución de análisis ANOVA individuales.
- Detecta patrones de respuestas multivariadas
- El factor puede afectar la relación entre las respuestas en lugar de afectar una respuesta individual. Los análisis de ANOVA no detectarán estos patrones multivariados como lo muestran las siguientes figuras.
- Controla la tasa de error por familia
- La probabilidad de rechazar de manera incorrecta la hipótesis nula aumenta con cada ANOVA sucesivo. La ejecución de un solo MANOVA para probar todas las variables de respuesta al mismo tiempo mantiene la tasa de error por familia igual a su nivel alfa.
Por ejemplo, está estudiando los efectos de diferentes aleaciones (1, 2 y 3) sobre la dureza y flexibilidad de los productos de construcción de su compañía. Primero ejecuta dos análisis ANOVA independientes, pero los resultados no son significativos. Al sorprenderle, crea la gráfica de los datos sin procesar para ambas variables de respuestas utilizando gráficas de valores individuales. Estas gráficas permiten confirmar visualmente estos resultados no significativos en el ANOVA.
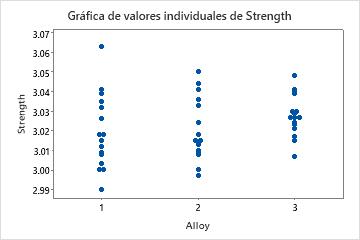
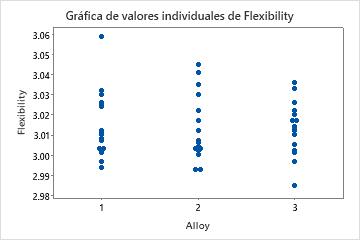
Debido a que las variables de respuesta están correlacionadas, usted ejecuta un análisis MANOVA. En esta oportunidad, los resultados son significativos, con valores p menores que 0.05. Usted crea una gráfica de dispersión para comprender mejor los resultados.
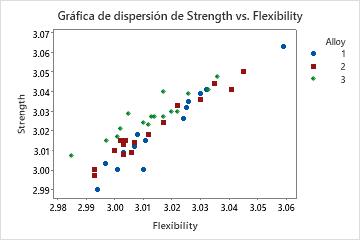
La gráfica de valores individuales muestra, desde una perspectiva univariada, que las aleaciones no afectan de manera significativa ni la dureza, ni la flexibilidad. Sin embargo, la gráfica de dispersión de los mismos datos muestra que las diferentes aleaciones cambian la relación entre las dos variables de respuesta. Es decir, para una puntuación de flexibilidad especificada, la aleación 3 generalmente tiene una puntuación de dureza más alta que las aleaciones 1 y 2. MANOVA puede detectar este tipo de respuestas multivariadas, mientras que ANOVA no puede lograrlo.
Nota
Por lo general, debería crear la gráfica de los datos antes de realizar cualquier análisis porque esta gráfica le ayudará a decidir cual enfoque es el más apropiado.
¿Cuáles pruebas multivariadas están incluidas en MANOVA?
- Prueba de Wilk
- Prueba de Lawley-Hotelling
- Prueba de Pillai
- Prueba de la raíz más grande de Roy
- Una matriz de H (hipótesis) asociada con cada término, también denominada sumas de cuadrados entre muestras
- Una matriz de E (error) asociada con el error para la prueba; también denominada sumas de cuadrados dentro de muestras
Las matrices SSCP se muestran cuando se solicita las matrices de hipótesis.
Se pueden expresar los estadísticos de prueba como H, E o H y E, o como valores propios de E-1 H.. Se puede solicitar que sean mostrados estos valores propios. (Si se repiten los valores propios, los vectores propios correspondientes no son únicos y, en este caso, los vectores propios que Minitab muestra y los que se encuentran en los libros, o en cualquier otro software, pudieran no coincidir. Sin embargo, las pruebas de MANOVA, no siempre son únicas.)
