¿Qué es una covariable?
Las covariables se utilizan generalmente en ANOVA y DOE. En estos modelos, una covariable es cualquier variable continua, que usualmente no se controla durante la recogida de datos. Incluyendo las covariables, el modelo permite incluir y adaptar las variables de entrada que se midieron pero no se aleatorizaron o controlaron en el experimento. Al agregar covariables se puede mejorar considerablemente la exactitud del modelo y se puede afectar significativamente los resultados del análisis final. Incluyendo una covariable en el modelo se puede reducir el error en el modelo para incrementar la potencia de las pruebas de los factores. Las covariables comunes incluyen temperatura ambiente, humedad y características de una parte o sujeto antes de aplicar un tratamiento.
Por ejemplo, un ingeniero desea estudiar el nivel de corrosión en cuatro tipos de vigas de hierro. El ingeniero expone cada viga a un tratamiento con líquido para acelerar la corrosión, pero no puede controlar la temperatura del líquido. La temperatura es una covariable que se debería considerar en el modelo.
En un DOE, un ingeniero puede estar interesado en el efecto de la covariable temperatura ambiente sobre el tiempo de secado de dos diferentes tipos de pintura.
Ejemplo de adición de una covariable a un modelo lineal general
Una empresa textil utiliza tres máquinas diferentes para producir fibras monofilamento. Ellos desean determinar si la resistencia a la rotura de la fibra varía dependiendo de la máquina que se utiliza. Recogen datos sobre la resistencia y el diámetro de 5 fibras seleccionadas de forma aleatoria de cada máquina. Como la resistencia de la fibra está relacionada con su diámetro, también registran el diámetro de la fibra para usarlo como una posible covariable.
| C1 | C2 | C3 |
|---|---|---|
| Máquina | Diámetro | Resistencia |
| 1 | 20 | 36 |
| 1 | 25 | 41 |
| 1 | 24 | 39 |
| 1 | 25 | 42 |
| 1 | 32 | 49 |
| 2 | 22 | 40 |
| 2 | 28 | 48 |
| 2 | 22 | 39 |
| 2 | 30 | 45 |
| 2 | 28 | 44 |
| 3 | 21 | 35 |
| 3 | 23 | 37 |
| 3 | 26 | 42 |
| 3 | 21 | 34 |
| 3 | 15 | 32 |
- Verifique que la covariable y la respuesta estén linealmente relacionadas. Esto se puede hacer en Minitab al analizar los datos con una gráfica de línea ajustada.
- Elija .
- En Respuesta(Y) ingrese Resistencia.
- En Predictor(X) ingrese Diámetro.
- Evalúe que tan cerca quedan los datos de la línea ajustada y qué tan cerca está el R2 de un "ajuste perfecto" (100%).
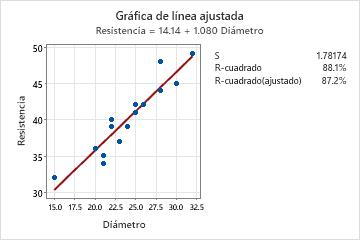
La gráfica de línea ajustada indica una fuerte relación lineal (87.2%) entre el diámetro y la resistencia.
- Realice el análisis de GLM con la covariable.
- Elija .
- En Respuestas, ingrese Resistencia.
- En Factores, ingrese Máquina.
- En Covariables, ingrese Diámetro.
- Haga clic en Aceptar.
Para los datos de producción de fibras, Minitab muestra los siguientes resultados:
Modelo lineal general: Resistencia vs. Diámetro, Máquina
Análisis de Varianza Fuente GL SC Ajust. MC Ajust. Valor F Valor p Diámetro 1 178.014 178.014 69.97 0.000 Máquina 2 13.284 6.642 2.61 0.118 Error 11 27.986 2.544 Falta de ajuste 7 18.486 2.641 1.11 0.487 Error puro 4 9.500 2.375 Total 14 346.400El estadístico F para máquinas es de 2.61 y el valor p es de 0.118. Puesto que el valor p >0.05, no puede rechazar la hipótesis nula de que las resistencias de las fibras no difieren dependiendo de la máquina utilizada en el nivel de significancia de 5%. Se puede presuponer que las resistencias de las fibras son iguales en todas las máquinas. Observe que el estadístico F para diámetro (covariable) es de 69.97, con un valor p de 0.00. Esto indica que el efecto de la covariable es significativo. Es decir, el diámetro tiene un impacto estadísticamente significativo en la resistencia de la fibra.
Ahora, supongamos que usted vuelve a ejecutar el análisis y omite la covariable. Esto dará como resultado la siguiente salida:
Modelo lineal general: Resistencia vs. Máquina
Análisis de Varianza Fuente GL SC Ajust. MC Ajust. Valor F Valor p Máquina 2 140.4 70.20 4.09 0.044 Error 12 206.0 17.17 Total 14 346.4Observe que el estadístico F es de 4.09 con un valor p de 0.044. Sin la covariable en el modelo, se rechaza la hipótesis nula en el nivel de significancia de 5% y se concluye que las resistencias de las fibras sí difieren dependiendo de la máquina que se utiliza.
Esta conclusión es totalmente opuesta a la conclusión a la que se llegó cuando realizó el análisis con la covariable. Con este ejemplo se demuestra cómo el hecho de no incluir una covariable puede producir resultados de análisis engañosos.
