Acerca del mensaje "deficiencia de rango"
Los modelos lineales son de rango completo cuando el número de observaciones por cada combinación de niveles de factor es adecuado para poder estimar todos los términos incluidos en el modelo. Cuando no hay suficientes observaciones en los datos para ajustar el modelo, Minitab elimina términos hasta que el modelo es lo suficientemente pequeño para ajustarse. Es posible que otros modelos puedan ajustarse mejor a los datos.
Supongamos que usted tiene un modelo GLM de dos factores. Intenta ajustar el modelo con los términos A B y A*B, pero recibe un mensaje de error sobre una "deficiencia de rango". Esto indica que no hay suficientes observaciones por cada combinación de los niveles de los factores. Pruebe eliminando el término de interacción (A*B).
¿Qué es deficiencia de rango?
Deficiencia de rango es una condición que puede impedir que Minitab realice cálculos de matriz. Por ejemplo, consideremos el siguiente conjunto de datos con dos variables predictoras y una variable de respuesta:
| C1 | C2 | C3 |
|---|---|---|
| X1 | X2 | Y |
| 1,5 | 9,7 | 15,0 |
| 1,4 | 8,4 | 14,0 |
| 1,6 | 8,6 | 16,0 |
| 1,7 | 8,9 | 17,0 |
| 1,7 | 8,1 | 14,5 |
X1 y X2 son las variables predictoras y Y es la variable de respuesta. El análisis de regresión de Minitab utiliza los mínimos cuadrados para calcular los coeficientes estimados b0, b1, b2, en la siguiente ecuación lineal:
Y = b0 + b1X1 + b2X2
El procedimiento de mínimos cuadrados es equivalente a resolver el conjunto de ecuaciones de matriz
b = (XTX)-1XTY
donde b es un vector de columna que contiene los coeficientes estimados del modelo, X es una matriz cuya primera columna es una columna de unos (utilizada para estimar la intersección/constante) y cuyas columnas restantes son las columnas de datos predictores (X1, X2,...) y Y es el vector columna de datos de respuesta. Para el conjunto de datos anterior, las matrices son:
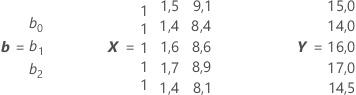
Minitab utiliza la descomposición QR para calcular las estimaciones de los parámetros (b0, b1 y b2) y las desviaciones estándar de los parámetros. El cálculo depende de los valores propios de la matriz (XTX). Si algunos de los valores propios de (XTX) son esencialmente cero, la matriz cuadrada (XTX) es singular o está de ser singular y Minitab no podrá hacer los cálculos.
¿Qué causa la deficiencia de rango?
La deficiencia de rango se produce si hay columnas de variables X que pueden escribirse como una combinación lineal de las demás columnas X. Se muestran dos ejemplos, usando C1, C2 y C3 como las variables predictoras (X):
Example 1
| C1 | C2 | C3 |
|---|---|---|
| X1 | X2 | X3 |
| 1 | 2 | 3 |
| 2 | 3 | 5 |
| 1,5 | 2,5 | 4 |
Example 2
| C1 | C2 | C3 |
|---|---|---|
| X1 | X2 | X3 |
| 1 | 2 | 3 |
| 2 | 4 | 5 |
| 1,5 | 3 | 4 |
En el primer ejemplo, note que C1 + C2 = C3.
En el segundo ejemplo, note que 2*C1 = C2.
Si intenta hacer una regresión (o ANOVA) usando estos predictores, Minitab eliminará términos del modelo para poder realizar el análisis.
La deficiencia de rango también puede producirse con datos categóricos:
Example 3
| C1 | C2 | C3 |
|---|---|---|
| Máquina | Operador | Respuesta |
| 1 | Joel | 15 |
| 1 | Joel | 18 |
| 1 | Joel | 17 |
| 2 | Bill | 14 |
| 2 | Bill | 15 |
| 2 | Bill | 16 |
En este ejemplo, observe que la columna Máquina tiene exactamente el mismo patrón que la columna Operador. Si usted realiza un ANOVA con este conjunto de datos, Minitab eliminará términos del modelo para poder realizar el análisis.
- Un término de interacción incluido no tiene al menos una observación para cada combinación de los niveles de los factores. Por ejemplo, si A tiene 3 niveles, B tiene 4 niveles y usted incluya la interacción A*B en el modelo sin tener al menos una observación para las 12 combinaciones de los niveles de los factores.
- Existe anidación no balanceada.
- Una variable continua presente en el modelo no está especificada como covariable.
- Los grados de libertad para el error son negativos.
