En este tema
Paso 1: Estimar la desviación estándar para cada población
Utilice los intervalos de confianza de Bonferroni para estimar la desviación estándar de cada población basándose en sus factores categóricos. Cada intervalo de confianza es un rango de valores probables para la desviación estándar de la población correspondiente.
Minitab ajusta los intervalos de confianza de Bonferroni para mantener el nivel de confianza simultáneo. Con los intervalos de confianza de Bonferroni de 95 %, se puede estar un 95 % seguro de que todo el conjunto de intervalos de confianza incluye las verdaderas desviaciones estándar de población para todos los grupos.
Controlar los intervalos de confianza simultáneos es especialmente importante cuando se realizan comparaciones múltiples. Si no se controla el intervalo de confianza simultáneo, la probabilidad de que por lo menos un intervalo de confianza no contenga la desviación estándar aumenta con el número de intervalos de confianza.
Nota
No se pueden utilizar los intervalos de confianza de Bonferroni para determinar si las diferencias entre los pares de grupos son estadísticamente significativas. Para determinar la significancia estadística de las diferencias entre los pares de grupos, utilice los intervalos de comparación múltiple en el paso 2.
Para obtener más información, vaya a Uso de los niveles de confianza para identificar diferencias significativas entre los niveles de los factores en las comparaciones múltiples y a ¿Cuál es el método Bonferroni?.
Método
| Hipótesis nula | Todas las varianzas son iguales |
|---|---|
| Hipótesis alterna | Por lo menos una varianza es diferente |
| Nivel de significancia | α = 0.05 |
Intervalos de confianza de Bonferroni de 95% para desviaciones estándar
| Fertilizante | N | Desv.Est. | IC |
|---|---|---|---|
| GrowFast | 50 | 4.28743 | (3.43659, 5.61790) |
| Ninguno | 50 | 5.09137 | (4.24793, 6.40914) |
| SuperPlant | 49 | 5.49969 | (4.48577, 7.08914) |
Resultados clave: Desv.Est. Intervalos de confianza de Bonferroni de 95 %, Nivel de confianza individual
En estos resultados, los intervalos de confianza de Bonferroni indican que se puede estar un 95 % seguro de que todo el conjunto de intervalos de confianza incluye las verdaderas desviaciones estándar de población para todos los grupos. También, el nivel de confianza individual indica qué tan seguro se puede estar de que un intervalo de confianza individual contenga la desviación estándar de población de ese grupo específico. Por ejemplo, se puede estar un 98.3333 % seguro de que la desviación estándar para la población GrowFast está dentro del intervalo de confianza (3.43659, 5.61790).
Paso 2: Determinar si las desviaciones estándar de población son diferentes
Utilice la gráfica de resumen para determinar si cualquiera de las diferencias entre las desviaciones estándar es estadísticamente significativa. Los tipos de pruebas e intervalos que Minitab muestra dependen de si se marcó Utilice la prueba basándose en la distribución normal en el subcuadro de diálogo Opciones y en el número de grupos en sus datos.
- Valores p de las pruebas
-
Utilice los valores p en la gráfica de resumen para determinar si cualquiera de las diferencias entre las desviaciones estándar es estadísticamente significativa. Minitab muestra los resultados de una o dos pruebas que evalúan la igualdad de varianzas. Si tiene dos valores p y no coinciden, vaya a Todos los estadísticos y gráficas y haga clic en "Pruebas" para obtener información sobre cuál de las pruebas utilizar.
Compare el valor p con el nivel de significancia para evaluar la hipótesis nula. La hipótesis nula es que las desviaciones estándar grupales son todas iguales. Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que existe una diferencia cuando no hay una diferencia real.
Utilice las siguientes directrices para interpretar los valores p:- Si el valor p es > α, las diferencias entre las desviaciones estándar no son estadísticamente significativas.
- Si el valor p es ≤ α, las diferencias entre algunas de las desviaciones estándar son estadísticamente significativas.
- Intervalos de comparaciones múltiples
-
Si no se seleccionó Utilice la prueba basándose en la distribución normal, la gráfica resumen muestra los intervalos de confianza para el método de comparaciones múltiples. Por lo general, las conclusiones se pueden basar en la prueba de comparaciones múltiples y los intervalos de comparación múltiple, a menos que se tengan muestras pequeñas de distribuciones muy asimétricas, o distribuciones con colas pesadas.
Utilice los intervalos de comparación múltiple para identificar los pares específicos de desviaciones estándar que no son iguales. Si dos intervalos no se sobreponen, la diferencia entre las desviaciones estándar correspondiente es estadísticamente significativa. Si el valor p para la prueba de comparaciones múltiples es menor que el nivel de significancia, al menos un par se intervalos no se sobrepone.
- Intervalos de confianza de Bonferroni
-
Si se seleccionó Utilice la prueba basándose en la distribución normal, la gráfica de resumen muestra los intervalos de confianza de Bonferroni para estimar la desviación estándar de cada población. No se pueden utilizar estos intervalos para determinar si las diferencias entre los pares grupales son estadísticamente significativas. Vaya al paso 1 para obtener más información acerca de cómo interpretar los intervalos de confianza de Bonferroni.
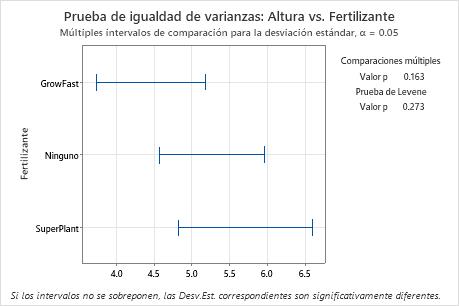
Resultados clave: Valor p de las Comparaciones múltiples
En esta gráfica de resumen, el valor p de la prueba de comparaciones múltiples es mayor que el nivel de significancia de 0.05. Ninguna de las diferencias entre los grupos son estadísticamente significativas y todos los intervalos de comparación se sobreponen.
