En este tema
Valor ajustado condicional
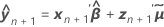
Notación
| Término | Description |
|---|---|
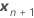 | el vector de los nuevos valores para los términos de efecto fijo |
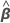 | los coeficientes estimados para los términos de efecto fijo |
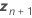 | El vector de los nuevos valores para los términos aleatorios |
 | las predicciones BLUP para los términos aleatorios |
Error estándar del valor ajustado condicional (EE ajuste)
El error estándar de un valor ajustado condicional es igual a la raíz cuadrada de la siguiente expresión de varianza.
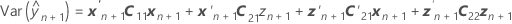
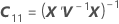
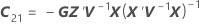

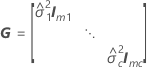
X es la matriz de diseño para los términos de efecto fijo y Z es la matriz de diseño para los términos aleatorios.
Intervalos de confianza para las medias condicionales
El rango en el que se espera que se encuentre la respuesta media para un conjunto dado de valores predictores.
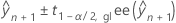
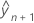 es el ajuste condicional.
es el ajuste condicional. 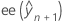 es el error estándar del ajuste.
es el error estándar del ajuste.
Los grados de libertad utilizan esta fórmula para el caso condicional:
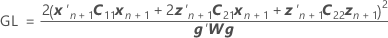
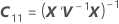
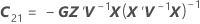

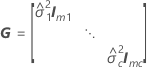
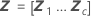
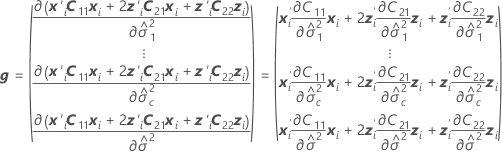



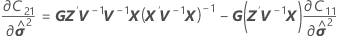
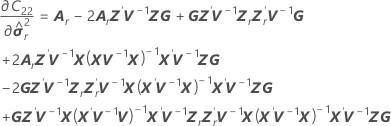
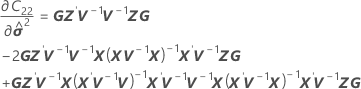
Notación
| Término | Description |
|---|---|
| W | la matriz asintótica de varianzas-covarianzas de 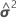 |
Para obtener más información sobre la notación, vaya a Ajustes y residuos condicionales en Ajustar modelo de efectos mixtos.
Intervalo de predicción condicional
El intervalo de predicción condicional es:

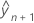 es el ajuste condicional con el nuevo valor de la variable.
es el ajuste condicional con el nuevo valor de la variable.
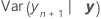 =
= 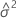
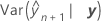 =
= 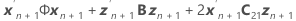
Los grados de libertad utilizan esta fórmula para el caso condicional:
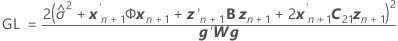
donde
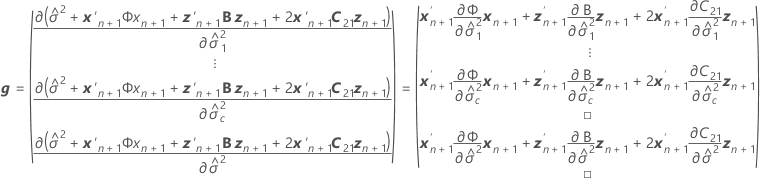
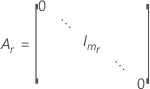
Notación
| Término | Description |
|---|---|
| W | la matriz asintótica de varianzas-covarianzas de las estimaciones de los componentes de la varianza |
| I | la matriz de identidad |
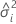 | el componente de la varianza para el iésimo término de efecto aleatorio |
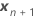 | el vector de los nuevos valores para los términos de efecto fijo |
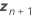 | el vector de los nuevos valores para los términos de efecto aleatorio |
| c | el número de términos aleatorios incluidos en el modelo |
| B |
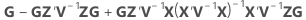 |
 |
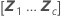 |
| C21 |
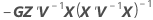 |
| G |
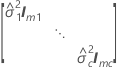 |
| mi | el número de niveles para el  efecto aleatorio efecto aleatorio |
| X | la matriz de diseño n x p para los términos de efectos fijos,  |
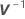 | la inversa de la matriz de varianzas-covarianzas |
 | la matriz de diseño n x mi para el  término aleatorio incluido en el modelo término aleatorio incluido en el modelo |
