Notación
| Término | Description |
|---|---|
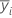 | la media de la muestra para el iésimo nivel del factor |
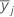 | la media de la muestra jesimo nivel del factor |
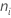 | el número de observaciones en el nivel i |
| r | el número de niveles |
| s | la desviación estándar agrupada o raíz cuadrada (MSE) |
| u | los grados de libertad para el error |
| α | la probabilidad simultánea de cometer un error de tipo I) |
| α* | la probabilidad individual de cometer un error de tipo I |
Tukey:
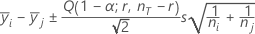
donde Q = percentil α superior de la distribución de rango estudentizado con r y nT - r grados de libertad.
Para encontrar la tasa de error individual a partir de la tasa de error simultánea, utilice la fórmula siguiente:

Fisher:
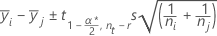
donde t = el punto α/2 superior de la distribución t de Student con u df.
Para encontrar el nivel de confianza simultáneo a partir de la tasa de error individual, utilice la fórmula siguiente:

Dunnett:

Para ver cómo se calcula d, rémitase a la página 63 en Hsu1.
MCB de Hsu:
Damos fórmulas para el caso donde todos los tamaños de grupo son iguales a n. Las fórmulas para tamaños de grupos que no son iguales se encuentran en Hsu1. Supongamos que elige el mejor para que sea la media más grande y desea que el intervalo de confianza de la iésima media menos la más grande de las otras.
El extremo inferior es el más pequeño de cero y

El extremo superior es el más grande de cero y

Para ver cómo se calcula d, remítase a la página 83 en Hsu1.
Cuando la mejor es la más pequeña de las medias de nivel, las fórmulas son las mismas, excepto que la máxima es reemplazada por la mínima.
Prueba de Welch y Games-Howell
El estadístico de prueba de Welch es calculado de la manera siguiente.
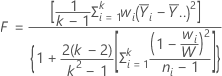
El valor p para la prueba de Welch es una probabilidad superior de cola para una distribución F con grados de libertad de numerador k - 1, donde k es el número de niveles X y grados de libertad de denominador dados por:
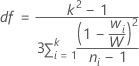
El intervalo de comparación de μi - μj es
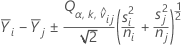
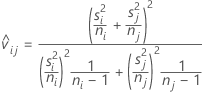
La relación t usada para calcular el valor P ajustado equivale a:
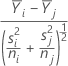
Donde:
La jésima respuesta en el iésimo nivel del factor categórico equivale a:Yij, j = 1, ... , ni; i = 1, ... k
La respuesta promedio en el iésimo nivel equivale a:
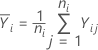
La varianza de la muestra equivale a:
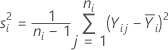
El peso del nivel i equivale a:
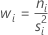
La suma de todos los pesos equivale a:
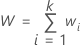
El promedio de respuestas general ponderado equivale a:
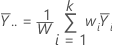
Reconocimiento
Estamos muy agradecidos por la asistencia en el diseño e implementación de comparaciones múltiples de Jason C. Hsu.
[1] J.C. Hsu (1996). Multiple Comparisons, Theory and methods. [Comparaciones múltiples, Teoría y métodos] Chapman & Hall.
