En este tema
Notación
La notación es crítica para entender los modelos de ANOVA. A continuación, encontrará la notación usada para los análisis de varianza de un solo factor.
| Término | Description |
|---|---|
| r | número de niveles del factor, i = 1 ...r |
| i | un nivel de factor determinado |
| j | un caso dado para un nivel de factor particular, j = 1 ...ni |
| yij | jésima observación de la respuesta para el iésimo nivel del factor |
| ni | número de observaciones para el iésimo nivel del factor |
| nT | número total de casos |
| μi | media real de observaciones al iésimo nivel del factor |
| yi. | total de las observaciones al iésimo nivel del factor |
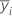 | media de la respuesta del iiésimo factor |
Ajuste del modelo
Fórmula
El análisis de un solo factor del modelo de varianza se puede especificar de diferentes maneras. El modelo de medias de celda es:
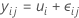
Todas las observaciones para el nivel de factor tienen la misma expectativa, μi. Puesto que μi es una constante, todas las observaciones tienen la misma varianza, independientemente del nivel de factor.
En el análisis de varianza, la estimación de los cuadrados mínimos se usa para ajustar el modelo y proporcionar estimaciones para los parámetros, μi.
La prueba de hipótesis de un análisis de varianza de un solo factor es:
H0: μ1 = μ2= … = μr
H1: Al menos una media no es igual a las otras
Notación
| Término | Description |
|---|---|
| μi | parámetros o la media real de observaciones al iésimo nivel del factor |
| εij | error que está independiente y normalmente distribuido con una media de 0 y una varianza constante de σ2 |
