Métodos y fórmulas para el análisis de varianza en ANOVA de un solo factor

Seleccione el método o la fórmula de su preferencia.

En este tema

Grados de libertad (GL)
Suma de los cuadrados (SC)
Cuadrados medios (CM)
Valor F
Valor p
S
R-cuad.
R-cuad.(ajustado)
R-cuad.(pred)

Grados de libertad (GL)

Fórmula

Indica el número de elementos independientes en la suma de cuadrados. Los grados de libertad para cada componente del modelo son:

(Factor) GL = r – 1
Error GL = n_T – r
Total = n_T – 1

Notación

Término	Description
n_T	número total de observaciones
r	Número de niveles de factor

Suma de los cuadrados (SC)

Fórmula

La suma de las distancias al cuadrado. La SC Total es la variación total en los datos. El SC (Factor) es la desviación de la media del nivel de factor estimado alrededor de la media general. Esto se conoce también como la suma de los cuadrados entre los tratamientos. El error SC es la desviación de una observación desde su media de nivel de factor correspondiente. Esto se conoce también como error en los tratamientos.

Los cálculos son:

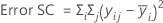
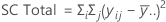
Notación

Término	Description
y̅_i_.	media de observaciones en el i^ésimo nivel del factor
y̅..	media de todas las observaciones
y_ij	valor de la j^ésima observación al i^ésimo nivel del factor

Cuadrados medios (CM)

Fórmula

El cálculo del cuadrado medio del factor sigue:

El cálculo del cuadrado medio del error sigue:

Notación

Término	Description
CM	Cuadrado medio
SC	Suma de los cuadrados
GL	Grados de libertad

Valor F

Fórmula

Los grados de libertad del numerador son r – 1. Los grados de libertad del denominador son n_T – r.

Notación

Término	Description
n_T	número total de observaciones
r	número de niveles del factor

Valor p

Se utiliza en las pruebas de hipótesis como ayuda para decidir si se puede rechazar o no una hipótesis nula. El valor p es la probabilidad de obtener una estadística de prueba que sea por lo menos tan extrema como el valor calculado real, si la hipótesis nula es verdadera. Un valor de corte comúnmente utilizado para el valor p calculado es 0.05. Por ejemplo, si el valor p de una estadística de prueba es menor que 0.05, rechace la hipótesis nula.

S

Un estimado de σ, la medida de la desviación estándar dentro de una muestra. Observe que S² = Error de CM. Esto es equivalente a la desviación estándar agrupada usada en el cálculo de los intervalos de confianza individuales.

R-cuad.

Otra presentación de la fórmula es:

R² también se puede calcular como la correlación cuadrada de y y .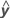

Notación

Término	Description
SC	Suma de los cuadrados
y	variable de respuesta
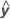	variable de respuesta ajustada

R-cuad.(ajustado)

Notación

Término	Description
CM	Cuadrado medio
SC	Suma de los cuadrados
GL	Grados de libertad

R-cuad.(pred)

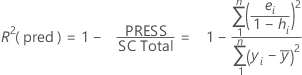
Aunque los cálculos de R²(pred) pueden producir valores negativos, para estos casos Minitab muestra cero.

Notación

Término	Description
y_i	i ^ésimo valor de respuesta observado
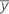	respuesta media
n	número de observaciones
e_i	i ^ésimo residuo
h_i	i ^ésimo elemento diagonal de X(X'X)^–1X'
X	matriz de diseño