En este tema
- Paso 1: Determinar si las diferencias entre las medias de los grupos son estadísticamente significativas
- Paso 2: Examinar las medias de los grupos
- Paso 3: Comparar las medias de los grupos
- Paso 4: Determinar hasta qué punto el modelo se ajusta a sus datos
- Paso 5: Determinar si el modelo cumple con los supuestos del análisis
Paso 1: Determinar si las diferencias entre las medias de los grupos son estadísticamente significativas
- Valor p ≤ α: Las diferencias entre algunas de las medias son estadísticamente significativas
- Si el valor p es menor que o igual al nivel de significancia, usted rechaza la hipótesis nula y concluye que no todas las medias de población son iguales. Utilice su conocimiento especializado para determinar si las diferencias son significativas desde el punto de vista práctico. Para obtener más información, vaya a Significancia estadística y significancia práctica.
- Valor p > α: Las diferencias entre las medias no son estadísticamente significativas
- Si el valor p es mayor que el nivel de significancia, usted no cuenta con suficiente evidencia para rechazar la hipótesis de que las medias de población son todas iguales. Verifique que la prueba tenga suficiente potencia para detectar una diferencia que sea significativa desde el punto de vista práctico. Para obtener más información, vaya a Aumentar la potencia de una prueba de hipótesis.
Análisis de Varianza
| Fuente | GL | SC Ajust. | MC Ajust. | Valor F | Valor p |
|---|---|---|---|---|---|
| Pintura | 3 | 281.7 | 93.90 | 6.02 | 0.004 |
| Error | 20 | 312.1 | 15.60 | ||
| Total | 23 | 593.8 |
Resultado clave: Valor p
En estos resultados, la hipótesis nula establece que los valores de dureza media de 4 pinturas diferentes son iguales. Puesto que el valor p es menor que el nivel de significancia de 0,05, usted puede rechazar la hipótesis nula y concluir que algunas de las pinturas tienen medias diferentes.
Paso 2: Examinar las medias de los grupos
Use la gráfica de intervalo para mostrar la media y el intervalo de confianza para cada grupo.
- Cada punto representa una media de muestra.
- Cada intervalo es un intervalo de confianza de 95 % de la media de un grupo. Usted puede estar 95% seguro de que una media de grupo está dentro del intervalo de confianza del grupo.
Important
Interprete cuidadosamente estos intervalos porque hacer comparaciones múltiples aumenta la tasa de error de tipo 1. Es decir, cuando se aumenta el número de comparaciones, también se incrementa la probabilidad de que al menos una comparación concluirá de forma incorrecta que una de las diferencias observadas es significativamente diferente.
Para evaluar las diferencias que aparecen en esta gráfica, utilice la tabla Información de agrupación y otros resultados de comparación (como se muestra en el paso 3).
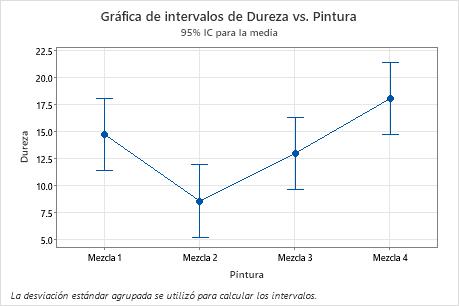
En la gráfica de intervalo, la Mezcla 2 tiene la media más baja y la Mezcla 4 tiene la más alta. Usted no puede determinar, con base en esta gráfica, si algunas de las diferencias son estadísticamente significativas. Para determinar la significancia estadística, evalúe los intervalos de confianza de las diferencias medias.
Paso 3: Comparar las medias de los grupos
Si el valor p del ANOVA de un solo factor es menor que el nivel de significancia, usted sabrá que algunas de las medias de los grupos son diferentes, pero no cuáles pares de grupos. Utilice la tabla Información de agrupación y pruebe las diferencias de las medias para determinar si esas diferencias entre los pares específicos de grupos es estadísticamente significativa y para estimar qué tan diferentes son las medias.
Para obtener más información sobre los métodos de comparación, vaya a Uso de comparaciones múltiples para evaluar la significancia práctica y estadística.
- Tabla Información de agrupación
-
Utilice la tabla Información de agrupación para determinar rápidamente si la diferencia de las medias entre cualquier par de grupos es estadísticamente significativa.
Los grupos que no comparten una letra son significativamente diferentes.
- Pruebas para las diferencias de las medias
-
Utilice los intervalos de confianza para determinar los posibles rangos de las diferencias y para determinar si las diferencias son significativas desde el punto de vista práctico. La tabla muestra un conjunto de intervalos de confianza para la diferencia entre los pares de medias. La gráfica de intervalo para las diferencias de las medias muestra la misma información.
Los intervalos de confianza que no contienen el cero indican una diferencia en las medias que es estadísticamente significativa.
Dependiendo del método de comparación que elija, la tabla compara diferentes pares de grupos y muestra uno de los siguientes tipos de intervalos de confianza.-
Nivel de confianza individual
El porcentaje de veces que un solo intervalo de confianza incluye la diferencia real entre un par de medias de grupo si el estudio se repite múltiples veces.
-
Nivel de confianza simultáneo
El porcentaje de veces que un conjunto de intervalos de confianza incluye las diferencias reales de todas las comparaciones de grupos si el estudio se repite múltiples veces.
Controlar los intervalos de confianza simultáneos es particularmente importante cuando usted realiza comparaciones múltiples. Si no se controlan los intervalos de confianza simultáneos, la probabilidad de que al menos un intervalo de confianza no contenga la diferencia real aumenta con el número de comparaciones.
-
Para obtener más información, vaya a Explicación de los niveles de confianza simultáneos e individuales en las comparaciones múltiples.
Para obtener más información acerca de cómo interpretar los resultados de MCB de Hsu, vaya a ¿Qué son las comparaciones múltiples de Hsu con el mejor (MCB)?
Agrupar información utilizando el método de Tukey y una confianza de 95%
| Pintura | N | Media | Agrupación | |
|---|---|---|---|---|
| Mezcla 4 | 6 | 18.07 | A | |
| Mezcla 1 | 6 | 14.73 | A | B |
| Mezcla 3 | 6 | 12.98 | A | B |
| Mezcla 2 | 6 | 8.57 | B | |
Resultados clave: Media, Agrupación
En estos resultados, la tabla muestra que el grupo A contiene las Mezclas 1, 3 y 4 y el grupo B contiene las Mezclas 1, 2 y 3. Las Mezclas 1 y 3 están en ambos grupos. Las diferencias entre las medias que comparten una letra no son estadísticamente significativas. Las Mezclas 2 y 4 no comparten una letra, lo que indica que la Mezcla 4 posee una media significativamente mayor que la Mezcla 2.
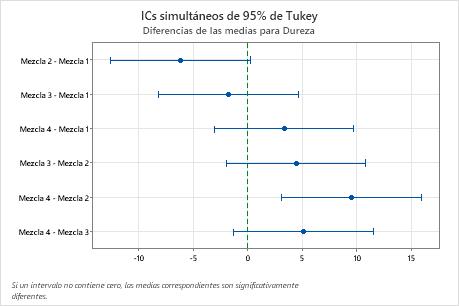
Pruebas simultáneas de Tukey para diferencias de las medias
| Diferencia de niveles | Diferencia de las medias | EE de diferencia | IC de 95% | Valor T | Valor p ajustado |
|---|---|---|---|---|---|
| Mezcla 2 - Mezcla 1 | -6.17 | 2.28 | (-12.55, 0.22) | -2.70 | 0.061 |
| Mezcla 3 - Mezcla 1 | -1.75 | 2.28 | (-8.14, 4.64) | -0.77 | 0.868 |
| Mezcla 4 - Mezcla 1 | 3.33 | 2.28 | (-3.05, 9.72) | 1.46 | 0.478 |
| Mezcla 3 - Mezcla 2 | 4.42 | 2.28 | (-1.97, 10.80) | 1.94 | 0.245 |
| Mezcla 4 - Mezcla 2 | 9.50 | 2.28 | (3.11, 15.89) | 4.17 | 0.002 |
| Mezcla 4 - Mezcla 3 | 5.08 | 2.28 | (-1.30, 11.47) | 2.23 | 0.150 |
Resultados clave: IC simultáneos de 95%, nivel de confianza individual
- El intervalo de confianza para la diferencia entre las medias de las Mezclas 2 y 4 es de 3.11 a 15.89. Este rango no incluye el cero, lo que indica que la diferencia es estadísticamente significativa.
- Los intervalos de confianza de los demás pares de medias incluyen el cero, lo que indica que las diferencias no son estadísticamente significativas.
- El nivel de confianza simultáneo de 95% indica que usted puede estar 95% seguro de que todos los intervalos de confianza contienen las diferencias reales.
- La tabla indica que el nivel de confianza individual es 98.94%. Este resultado indica que usted puede estar 98.94% seguro de que cada intervalo individual contiene la diferencia real entre un par específico de medias de grupo. Los niveles de confianza individuales de cada comparación producen el nivel de confianza simultáneo de 95% para las seis comparaciones.
Paso 4: Determinar hasta qué punto el modelo se ajusta a sus datos
Para determinar qué tan bien se ajusta el modelo a los datos, examine los estadísticos de bondad de ajuste en la tabla Resumen del modelo.
- S
- Utilice S para evaluar qué tan bien el modelo describe la respuesta.
S se mide en las unidades de la variable de respuesta y representa la distancia que separa a los valores de los datos de los valores ajustados. Mientras más bajo sea el valor de S, mejor describirá el modelo la respuesta. Sin embargo, un valor de S bajo no indica por sí solo que el modelo cumple con los supuestos del modelo. Debe examinar las gráficas de residuos para verificar los supuestos.
- R-cuad.
-
El R2 es el porcentaje de variación en la respuesta que es explicada por el modelo. Mientras mayor sea el valor de R2, mejor se ajustará el modelo a los datos. R2 siempre está entre 0% y 100%.
Un valor de R2 alto no indica que el modelo cumple con los supuestos del modelo. Debe examinar las gráficas de residuos para verificar los supuestos.
- R-cuad.(pred)
-
Utilice R2 pronosticado para determinar qué tan bien el modelo predice la respuesta para nuevas observaciones.Los modelos que tienen valores más grandes de R2 pronosticado tienen mejor capacidad de predicción.
Un R2 pronosticado que sea sustancialmente menor que R2 puede indicar que el modelo está sobreajustado. Un modelo sobreajustado se produce cuando se agregan términos para efectos que no son importantes en la población. El modelo se adapta a los datos de la muestra y, por lo tanto, es posible que no sea útil para hacer predicciones acerca de la población.
El R2 pronosticado también puede ser más útil que el R2 ajustado para comparar modelos, porque se calcula con observaciones que no se incluyen en el cálculo del modelo.
Resumen del modelo
| S | R-cuadrado | R-cuadrado(ajustado) | R-cuadrado (pred) |
|---|---|---|---|
| 3.95012 | 47.44% | 39.56% | 24.32% |
Resultados clave: S, R-cuad., R-cuad. (pred)
En estos resultados, el factor explica un 47.44 % de la variación en la respuesta. S indica que la desviación estándar entre los puntos de datos y los valores ajustados es de aproximadamente 3.95 unidades.
Paso 5: Determinar si el modelo cumple con los supuestos del análisis
Utilice las gráficas de residuos como ayuda para determinar si el modelo es adecuado y cumple con los supuestos del análisis. Si los supuestos no se cumplen, el modelo podría no ajustarse adecuadamente a los datos y se debería tener cuidado al interpretar los resultados.
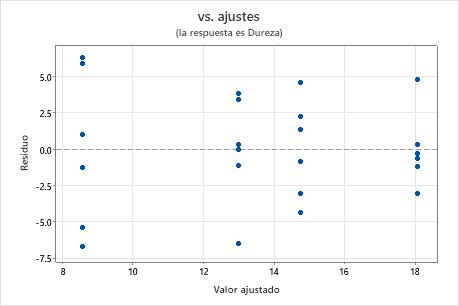
Gráfica de residuos vs. ajustes
Utilice la gráfica de residuos vs. ajustes para verificar el supuesto de que los residuos están distribuidos aleatoriamente y tienen una varianza constante. Lo ideal es que los puntos se ubiquen aleatoriamente a ambos lados del 0, con patrones no detectables en los puntos.
| Patrón | Lo que podría indicar el patrón |
|---|---|
| Dispersión en abanico o irregular de los residuos en los valores ajustados | Varianza no constante |
| Un punto que está alejado de cero | Un valor atípico |
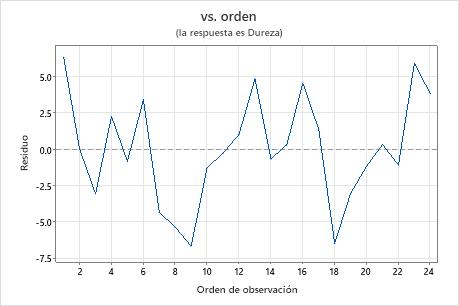
Gráfica de residuos vs. orden
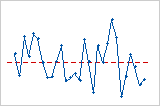
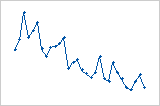
Tendencia
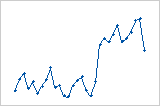
Cambio
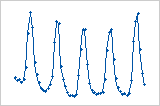
Ciclo
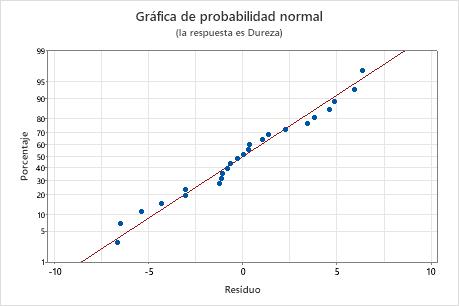
Gráfica de probabilidad normal de los residuos
Utilice la gráfica de probabilidad normal de los residuos para verificar el supuesto de que los residuos están distribuidos normalmente. La gráfica de probabilidad normal de los residuos debe seguir aproximadamente una línea recta.
| Patrón | Lo que podría indicar el patrón |
|---|---|
| No una línea recta | No normalidad |
| Un punto que está alejado de la línea | Un valor atípico |
| Pendiente cambiante | Una variable no identificada |
Nota
Si el diseño del ANOVA de un solo factor cumple con las directrices para el tamaño de la muestra, los resultados no se ven afectados sustancialmente por desviaciones con respecto a la normalidad.