En este tema
Componentes de la varianza
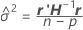
donde 

Para los detalles sobre la estimación de θi, consulte [1].
Para obtener más información sobre la notación, vaya a la sección Métodos.
Referencias
- Hemmerle, W. y Hartley, H. (1973). Computing Maximum Likelihood Estimates for the Mixed A.O.V. Model using the W transformation. Technometrics, 15(4):819–831.
Errores estándar de los componentes de la varianza
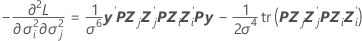
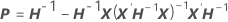
 columna, j = 1, …, c:
columna, j = 1, …, c:
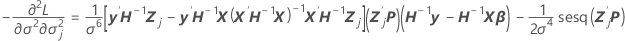

Este componente también es el valor de la última columna y la  fila por la propiedad de simetría de la matriz de varianzas-covarianzas.
fila por la propiedad de simetría de la matriz de varianzas-covarianzas.

La matriz asintótica de varianzas-covarianzas para las estimaciones de los componentes de la varianza es dos veces la inversa de la matriz de información observada de Fisher. Las estimaciones de los errores estándar son las raíces cuadradas de los elementos de la diagonal de la matriz de varianzas-covarianzas. Los primeros c elementos de la diagonal corresponden a los componentes de la varianza de los términos de efecto aleatorio. El último elemento de la diagonal corresponde al componente de la varianza del error.
Notación
| Término | Description |
|---|---|
 | la traza de la matriz  |
 | la suma de los cuadrados de todos los elementos de la matriz M |
Para obtener más información sobre la notación, vaya a la sección Métodos.
Intervalos de confianza para los componentes de la varianza
Minitab utiliza el método delta para construir límites de confianza de tipo Wald para el logaritmo natural de los componentes de la varianza, luego eleva a una potencia los intervalos de confianza para obtener los intervalos de confianza para los componentes de la varianza. Las fórmulas para el componente de la varianza para el error tienen la misma forma.
Intervalo bilateral
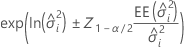
Borde inferior
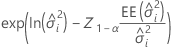
Borde superior
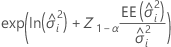
Notación
| Término | Description |
|---|---|
 | el cuantil 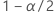 de la distribución normal estándar de la distribución normal estándar |
 | 1 − nivel de confianza |
 | el error estándar del  componente de la varianza componente de la varianza |
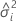 | el componente de la varianza para el  término de efecto aleatorio término de efecto aleatorio |
Valor Z y valor p
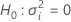
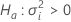


Notación
| Término | Description |
|---|---|
| Z | el valor de la función de distribución acumulada inversa para la distribución normal estándar |
Matriz de varianzas-covarianzas
 componente de la matriz de información observada de Fisher:
componente de la matriz de información observada de Fisher:
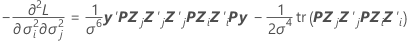

 columna, j = 1, …, c:
columna, j = 1, …, c:
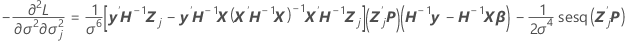

Este componente también es el valor de la última columna y la  fila por la propiedad de simetría de la matriz de varianzas-covarianzas.
fila por la propiedad de simetría de la matriz de varianzas-covarianzas.

Notación
| Término | Description |
|---|---|
 | la traza de la matriz  |
Para obtener más información sobre la notación, vaya a la sección Métodos.
