En este tema
Pruebas de los términos de efecto fijo
Las pruebas de los términos de efecto fijo son pruebas F. La hipótesis nula de la prueba depende de si la prueba es para un término de factor fijo o un término de covariable. Para un término de factor fijo, la hipótesis nula es que el término no afecta significativamente la respuesta. Para un término de covariable, la hipótesis nula es que no existe asociación entre la respuesta y el término de covariable.
Minitab ofrece 2 métodos para probar los términos de efecto fijo: la aproximación de Kenward-Roger y la aproximación de Satterthwaite. Para obtener más información sobre la aproximación de Kenward-Roger, consulte a Kenward y Roger.1 Para obtener más información sobre la aproximación de Satterthwaite, consulte a Giesbrecht y Burns 2 y a Fai y Cornelius. 3
El cálculo de los grados de libertad del denominador para el estadístico F y el cálculo del estadístico F son diferentes. El cálculo de los grados de libertad del numerador y la determinación de un valor p para un estadístico F dado son iguales para ambos métodos.
Aproximación de Kenward-Roger
La aproximación de Kenward-Roger es un método para probar la significancia estadística de los términos de efecto fijo.
Estadístico F
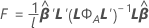
donde
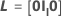
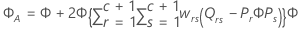
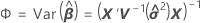
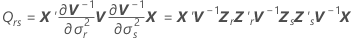
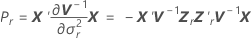
Notación
| Término | Description |
|---|---|
| l | los grados de libertad del numerador, que es el número de parámetros en el término que se probará |
| 0 | la matriz con 0 componentes |
| Il | la matriz de identidad con dimensión l |
| c + 1 | el número de componentes de la varianza |
| wrs | (r, s)ésimo componente de la matriz asintótica de varianzas-covarianzas de  |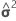
| V−1 | la inversa de la matriz de varianzas-covarianzas |
Para obtener más información sobre la notación, vaya a la sección Métodos.
Grados de libertad del denominador
donde
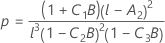
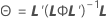
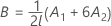
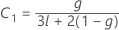
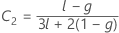
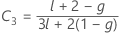
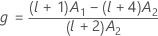
λ de Kenward y Roger
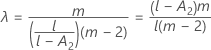
Si no se cumple una de las condiciones, entonces λ = 1.
Bajo la hipótesis nula, lambda × F sigue asintóticamente la distribución F con grados de libertad GL Num y GL Den. El cálculo del valor p utiliza esta propiedad.
Aproximación de Satterthwaite
La aproximación de Satterthwaite es un método para probar la significancia estadística de los términos de efecto fijo.
Estadístico F
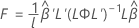
donde L y 
tiene las mismas definiciones que en la aproximación de Kenward-Roger.
Grados de libertad del denominador
El proceso para determinar los grados de libertad incluye varios pasos.
-
Realice la descomposición espectral sobre la varianza de la estimación del vector de parámetros de efecto fijo:
donde P es una matriz ortogonal de vectores propios y D es una matriz diagonal de valores propios, ambas con dimensión l × l.
-
Defina lr para que sea la résima fila de P'L, r = 1, ..., l y sea
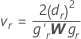donde dr es el résimo elemento de la diagonal de D, W es la matriz asintótica de varianzas-covarianzas de
y gr es el vector gradiente de los siguientes elementos:
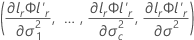
donde
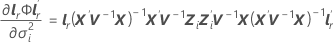
i = 1, …, c y
-
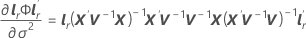
Sea
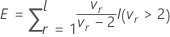
donde
es una función indicadora que elimina los términos con 
-
Los grados de libertad del denominador dependen del valor de E.
- Si E > l, entonces los grados de libertad son los siguientes:
- De lo contrario, GL Den = 1
- Si E > l, entonces los grados de libertad son los siguientes:
Grados de libertad del numerador (GL Num)
| Efecto | GL |
|---|---|
| Factor fijo |  |
| Covariable | 1 |
| Interacciones que incluyen factores fijos |  |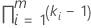
Notación
| Término | Description |
|---|---|
| k | el número de niveles en el término de factor fijo |
| m | el número de factores en la interacción |
Valor p – Pruebas de efectos mixtos
Notación
| Término | Description |
|---|---|
 | la función de distribución acumulada de la distribución F con grados de libertad iguales a GL Num y GL Den, respectivamente |
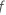 | el valor F calculado para un término |
