En este tema
El modelo de efectos mixtos y la log-verosimilitud
La forma general del modelo de efectos mixtos
Los modelos de efectos mixtos contienen efectos fijos y aleatorios. La forma general del modelo de efectos de efectos mixtos es:
y = Xβ + Z1μ1+ Z2μ2 + ... + Zcμc + ε
Notación
| Término | Description |
|---|---|
| y | el vector n x 1 de valores de respuesta |
| X | la matriz de diseño n x p para los términos de efectos fijos, p ≤ n |
| β | un vector p x 1 de parámetros desconocidos |
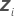 | la matriz de diseño n x mi para el  término aleatorio incluido en el modelo término aleatorio incluido en el modelo |
| μi | un vector mi x 1 de variables independientes desde N(0,  ) ) |
| ε | un vector n x 1 de variables independientes desde N(0,  ) ) |
| n | el número de observaciones |
| p | el número de parámetros en  |
| c | el número de términos aleatorios incluidos en el modelo |
Matriz de varianzas-covarianzas
De acuerdo con el supuesto del modelo para la forma general del modelo de efectos mixtos, el vector de respuestas, y, tiene una distribución normal multivariada con el vector de medias Xβ y la siguiente matriz de varianzas-covarianzas:
V(σ2) = V(σ2, σ21, ... , σ2c) = σ2In + σ21Z1Z'1 + ... + σ2cZcZ'c
donde
σ2 = (σ2, σ21, ... , σ2c)'
σ2, σ21, ... , σ2c se denominan componentes de la varianza.
Al factorizar a partir de la varianza, usted puede encontrar una representación de H(θ), que está en el cálculo de la log-verosimilitud de los modelos de efectos mixtos.
V(σ2) = σ2H(θ) = σ2[In + θ1Z1Z'1 + ... + θcZcZ'c]
Notación
| Término | Description |
|---|---|
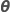 | 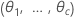 |
| θi | 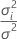 , la relación de la varianza del , la relación de la varianza del  término aleatorio sobre la varianza del error término aleatorio sobre la varianza del error |
Log-verosimilitud


Notación
| Término | Description |
|---|---|
| H | In + θ1Z1Z'1 + ... + θcZcZ'c |
| |H| | el determinante de H |
| H-1 | la inversa de H |
| mi | el número de niveles para el  término aleatorio término aleatorio |
 | el componente de la varianza del error |
| In | la matriz de identidad con n filas y columnas |
Estimación de máxima verosimilitud restringida (REML)
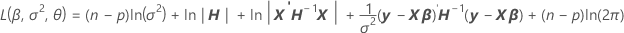
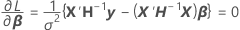
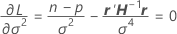
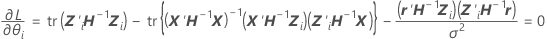
donde 
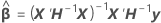
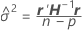
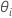 no se puede resolver explícitamente para los
no se puede resolver explícitamente para los 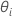 . Minitab utiliza el método de Newton para estimar
. Minitab utiliza el método de Newton para estimar 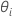 con los siguientes pasos:
con los siguientes pasos:
- Usar las estimaciones insesgadas de mínimos cuadrados bajo normalidad (MINQUE)12 de los componentes de la varianza para construir los valores iniciales de σ2 y θi.
- Estimar β y σ2 con las ecuaciones para
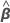 y
y 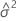 .
. - Hallar θi con el método de Newton para minimizar L(β, σ2, θ).
- Repetir los pasos 2 y 3 hasta la convergencia.
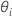 son las estimaciones de las relaciones de la varianza. El componente de la varianza para el
son las estimaciones de las relaciones de la varianza. El componente de la varianza para el  término aleatorio es el siguiente:
término aleatorio es el siguiente:

Notación
| Término | Description |
|---|---|
| tr(·) | la traza de la matriz |
| X' | la transpuesta de X |
