En este tema
Ajuste marginal
Los ajustes marginales representan las respuestas medias en diferentes niveles de los factores fijos. Los ajustes marginales se calculan a partir de las ecuaciones ajustadas marginales.
EE ajuste
El error estándar del ajuste (EE ajuste) estima la variación en la respuesta media estimada para la configuración especificada de las variables. El cálculo del intervalo de confianza para la respuesta media utiliza el error estándar del ajuste. Los errores estándar son siempre no negativos.
GL para la media marginal
Los grados de libertad (GL) representan la cantidad de información en los datos para estimar el intervalo de confianza para la respuesta media.
Interpretación
Utilice los GL para comparar la cantidad de información que está disponible acerca de las diferentes medias marginales. Por lo general, más grados de libertad hacen que el intervalo de confianza para la media sea más estrecho que un intervalo con menos grados de libertad. Puesto que los errores estándar para las medias de diferentes observaciones son diferentes, el intervalo de confianza para una media con más grados de libertad no tiene que ser más estrecho que un intervalo de confianza para una media con menos grados de libertad.
Intervalo de confianza para la media marginal (IC de 95%)
Estos intervalos de confianza (IC) son rangos de valores que es probable que contengan las respuestas medias marginales correspondientes.
Puesto que las muestras son aleatorias, es poco probable que dos muestras de una población produzcan intervalos de confianza idénticos. Sin embargo, si se toman muchas muestras, un determinado porcentaje de los intervalos de confianza resultantes incluirá el parámetro de población desconocido. El porcentaje de estos intervalos de confianza que contiene el parámetro es el nivel de confianza del intervalo.
El intervalo de confianza consta de las dos partes siguientes:
Interpretación
Utilice los intervalos de confianza para evaluar si las respuestas medias marginales son estadísticamente mayores que, iguales a o menores que un valor específico. También puede utilizar los intervalos de confianza para determinar un rango de valores para las respuestas medias marginales desconocidas correspondientes.
Residuos marginales
Un residuo (ei) es la diferencia entre un valor observado (y) y el valor ajustado marginal correspondiente, (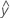 ).
).
Interpretación
Grafique los residuos para determinar si el modelo es adecuado y cumple con los supuestos del modelo de efectos mixtos. Examinar los residuos puede ofrecer información útil acerca de qué tan bien se ajusta el modelo a los datos. En general, los residuos deberían estar distribuidos aleatoriamente, sin patrones obvios ni valores poco comunes. Si Minitab determina que los datos incluyen observaciones poco comunes, identifica esas observaciones en la tabla Ajustes marginales y diagnósticos para observaciones poco comunes incluida en la salida. Las observaciones que Minitab etiqueta como poco comunes no siguen adecuadamente la ecuación marginal propuesta. Sin embargo, se espera que haya algunas observaciones poco comunes. Por ejemplo, con base en los criterios para los residuos grandes, se esperaría que aproximadamente el 5% de las observaciones sean marcadas como observaciones con un residuo grande.
Resid Est
El residuo marginal estandarizado es igual al valor de un residuo (ei) dividido entre una estimación de su desviación estándar.
Interpretación
Utilice los residuos marginales estandarizados como ayuda para detectar valores atípicos. Los residuos marginales estandarizados mayores que 2 y menores que −2 por lo general se consideran grandes. La tabla Ajustes marginales y diagnósticos para observaciones poco comunes identifica estas observaciones con una 'R'. Las observaciones que Minitab etiqueta no siguen adecuadamente la ecuación ajustada marginal propuesta. Sin embargo, se espera que haya algunas observaciones poco comunes. Por ejemplo, con base en los criterios para los residuos marginales estandarizados grandes, se esperaría que aproximadamente el 5% de las observaciones se marquen como observaciones con un residuo estandarizado grande.
Los residuos marginales estandarizados son útiles porque los residuos marginales sin procesar podrían no ser buenos indicadores de valores atípicos. La varianza de cada residuo marginal sin procesar puede diferir según los valores de X asociados al residuo. Esta variación desigual hace que sea difícil evaluar las magnitudes de los residuos marginales sin procesar. La estandarización de los residuos marginales resuelve este problema al convertir las diferentes varianzas a una escala común.
Hi (apalancamiento)
El apalancamiento (Hi) en un modelo de efectos mixtos puede utilizarse para identificar los puntos de los datos con altos valores de apalancamiento para los términos de efecto fijo solamente. La matriz de diseño que se utiliza para calcular Hi es la matriz de diseño para los términos de efecto fijo.
Interpretación
Los valores de Hi están entre 0 y 1. Minitab identifica las observaciones que tienen valores de apalancamiento mayores que 3p/n o 0.99, el valor que sea menor, con una X en la tabla Ajustes marginales y diagnósticos para observaciones poco comunes. En 3p/n, p es el número de coeficientes en el modelo y n es el número de observaciones. Las observaciones que Minitab etiqueta con una 'X' podrían ser influyentes.
Las observaciones influyentes tienen un efecto desproporcionado sobre el modelo y pueden generar resultados engañosos. Por ejemplo, la inclusión o exclusión de un punto influyente puede cambiar el hecho de que un coeficiente sea estadísticamente significativo o no. Las observaciones influyentes pueden ser puntos de apalancamiento, valores atípicos o ambos.
Si ve una observación influyente, determine si la observación es un error de entrada de datos o de medición. Si la observación no es un error de entrada de datos ni de medición, determine qué tan influyente es la observación. En primer lugar, ajuste el modelo con y sin la observación. Luego, compare los coeficientes, los valores p, el R2 y otras informaciones del modelo. Si el modelo cambia significativamente al eliminar la observación influyente, examine más a fondo el modelo para determinar si se especificó de forma incorrecta. Es posible que tenga que recopilar más datos para resolver el problema.
