Un investigador evalúa el rendimiento de seis variedades de alfalfa en cuatro campos seleccionados de forma aleatoria. El rendimiento de cada variedad se registró para cada campo.
El investigador desea saber si la variedad de alfalfa afecta el rendimiento medio. El investigador tiene 4 campos donde puede recopilar datos. Sin embargo, quiere poder modelar cómo crecerán las alfalfas en campos que no están incluidos en el experimento. Por lo tanto, el investigador hace que el campo donde crece la alfalfa sea un factor aleatorio. El investigador utiliza un modelo de efectos mixtos para evaluar los efectos fijos y aleatorios de forma conjunta.
- Abra los datos de muestra Alfalfa.MWX.
- Elija .
- En Respuestas, ingrese Rendimiento.
- En Factores aleatorios (obligatorio), ingrese Campo.
- En Factores fijos, ingrese Variedad.
- Haga clic en Gráficas.
- En Residuos para las gráficas, seleccione Condicionales estandarizados.
- En Gráficas de residuos, seleccione Cuatro en una.
- Haga clic en Aceptar en cada cuadro de diálogo.
Interpretar los resultados
En la tabla Componentes de la varianza, el valor p de Campo es 0.124. La prueba de hipótesis no muestra evidencia de que el componente de la varianza sea diferente de 0. El valor p para el componente de la varianza del error es 0.003. Puesto que el valor p es menor que el nivel de significancia de 0.05, el investigador puede concluir que el componente de la varianza del error no es 0.
El valor p de aproximadamente 0 para el término de factor fijo, Variedad, muestra que al menos el efecto de un tipo de alfalfa sobre el rendimiento es significativamente diferente de los otros cinco tipos.
Los coeficientes de los efectos principales representan la diferencia entre cada media de nivel y la media general. Por ejemplo, la Variedad 1 está asociada a un rendimiento de alfalfa que es aproximadamente de 0.385 unidades mayor que la media general. El valor p de aproximadamente 0 de este coeficiente indica que el efecto de la Variedad 1 en el rendimiento es significativamente diferente de otro efecto de nivel del término Variedad. Para determinar qué efectos de nivel son estadísticamente iguales y qué efectos de nivel son estadísticamente diferentes, el investigador planea hacer un análisis de comparación múltiple para el término.
El valor de R2 muestra que el modelo explica aproximadamente el 92% de la variación en el rendimiento. El valor de R-cuad. (ajust.) también es alto, con un valor de aproximadamente 90.2%. El investigador utiliza este valor para comparar modelos que tienen diferente número de predictores.
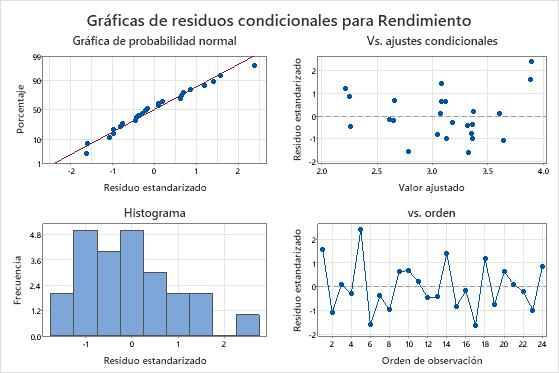
Las observaciones 1 y 5 son observaciones poco comunes, porque tienen residuos estandarizados mayores que 2. El investigador examina los datos para asegurarse de que los valores de respuesta de esas observaciones sean correctos.
Los residuos en la gráfica de probabilidad normal se aproximan a una línea recta, mientras que los puntos parecen estar dispersos alrededor del 0 en la gráfica de residuos vs. ajustes.
Método
| Estimación de la varianza | Máxima verosimilitud restringida |
|---|---|
| GL para efectos fijos | Kenward-Roger |
Información del factor
| Factor | Tipo | Niveles | Valores |
|---|---|---|---|
| Campo | Aleatorio | 4 | 1, 2, 3, 4 |
| Variedad | Fijo | 6 | 1, 2, 3, 4, 5, 6 |
Componentes de la varianza
| Fuente | Var | % del total | EE de la var. | Valor Z | Valor p |
|---|---|---|---|---|---|
| Campo | 0.077919 | 72.93% | 0.067580 | 1.152996 | 0.124 |
| Error | 0.028924 | 27.07% | 0.010562 | 2.738613 | 0.003 |
| Total | 0.106843 |
Pruebas de efectos fijos
| Término | GL Num | GL Den | Valor F | Valor p |
|---|---|---|---|---|
| Variedad | 5.00 | 15.00 | 26.29 | 0.000 |
Resumen del modelo
| S | R-cuadrado | R-cuadrado(ajustado) | AICc | BIC |
|---|---|---|---|---|
| 0.170071 | 92.33% | 90.20% | 12.54 | 13.52 |
Coeficientes
| Término | Coef | EE del coef. | GL | Valor T | Valor p |
|---|---|---|---|---|---|
| Constante | 3.094583 | 0.143822 | 3.00 | 21.516692 | 0.000 |
| Variedad | |||||
| 1 | 0.385417 | 0.077626 | 15.00 | 4.965016 | 0.000 |
| 2 | 0.145417 | 0.077626 | 15.00 | 1.873287 | 0.081 |
| 3 | 0.107917 | 0.077626 | 15.00 | 1.390205 | 0.185 |
| 4 | -0.319583 | 0.077626 | 15.00 | -4.116938 | 0.001 |
| 5 | 0.395417 | 0.077626 | 15.00 | 5.093838 | 0.000 |
Ajustes y diagnósticos marginales para observaciones poco comunes
| Obs | Rendimiento | Ajuste | Resid | Resid est. | |
|---|---|---|---|---|---|
| 1 | 4.100000 | 3.480000 | 0.620000 | 2.190221 | R |
| 5 | 4.220000 | 3.490000 | 0.730000 | 2.578808 | R |
Ajustes y diagnósticos condicionales para observaciones poco comunes
| Obs | Rendimiento | Ajuste | Resid | Resid est. | |
|---|---|---|---|---|---|
| 5 | 4.220000 | 3.895339 | 0.324661 | 2.400733 | R |