Un ingeniero desea evaluar la relación entre el tiempo de sinterización y la resistencia a la compresión de tres metales diferentes. El ingeniero mide la resistencia a la compresión de cinco muestras de cada tipo de metal con cada tiempo de sinterización: 100 minutos, 150 minutos y 200 minutos.
El ingeniero realiza un modelo lineal general (GLM) ANOVA e incluye una gráfica de efectos principales en la salida.
- Abra los datos de muestra, TiempoSinterización.MWX.
- Elija .
- En Respuestas, ingrese Resistencia.
- En Factores, ingrese TiempoSinter y TipoMetal.
- Haga clic en Aceptar.
Interpretar los resultados
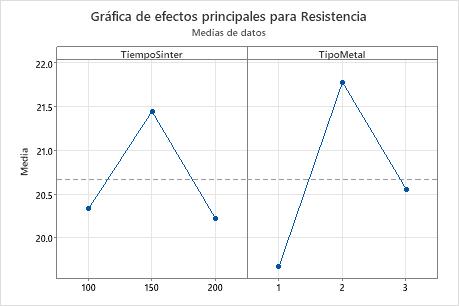
En este ejemplo, la gráfica de efectos principales muestra que el tipo de metal 2 está asociado con la resistencia más alta y que un tiempo de sinterización de 150 está asociado con la resistencia más alta. Sin embargo, los resultados del GLM indican que el efecto principal del tiempo de sinterización no es estadísticamente significativo. Las diferencias entre la resistencia media para los niveles del tiempo de sinterización pueden deberse a una probabilidad aleatoria.
Si se utiliza Ajustar modelo lineal general con este conjunto de datos, los resultados indican que la interacción entre el TiempoSinter y TipoMetal es estadísticamente significativa. Este efecto de interacción indica que la relación entre el tipo de metal y la resistencia depende del valor del tiempo de sinterización. En consecuencia, el ingeniero no puede interpretar los efectos principales sin considerar los efectos de interacción.
Aunque se puede utilizar esta gráfica para mostrar los efectos, también se debe evaluar la significancia estadística observando los efectos en una tabla de análisis de varianza.
Esta gráfica muestra medias de datos. Aunque se pueden utilizar las medias de datos para tener una idea general de cuáles efectos pudieran ser evidentes, por lo general es una buena práctica utilizar las medias ajustadas en Gráficas factoriales para obtener resultados más precisos.