Prueba de Wilk
El estadístico de prueba, lambda de Wilks, es:
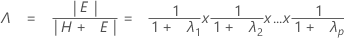
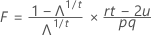
con pq y (rt – 2u) gl.
Notación
| Término | Description |
|---|---|
| H | matriz de hipótesis |
| E | matriz de error |
| p | número de respuestas |
| q | gl de la hipótesis |
| v | gl para E |
| s | mín (p, q) |
| m | .5 ( | p – q | – 1) |
| n | .5 (v – p – 1) |
| r | v – 0.5 (p – q + 1) |
| u | 0.25(pq – 2) |
| t | = raízcuad ([p2 q2 - 4] / p2 + q2 - 5, si p2 + q2 - 5 > 0 |
| t | 1 |
Sea λ1≥λ2≥λ3≥ . . . ≥λp siendo los valores propios de (E** - 1) * H.. Los primeros tres estadísticos de prueba pueden expresarse en términos de H y E o estos valores propios.
La matriz H es una matriz p x p que contiene la suma de cuadrados "entre" en la diagonal de cada una de las variables p.. La matriz H se calcula como:

La matriz E es una matriz p x p que contiene la suma de cuadrados "dentro" en la diagonal de cada una de las variables p.. La matriz E se calcula como:
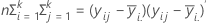
En las primeras tres pruebas, el estadístico F es exacto, si s = 1 ó 2; de lo contrario es aproximado. Minitab le dice cuando la prueba es aproximada.
Prueba de Lawley-Hotelling
El estadístico de prueba, el rastreo de Lawley-Hotelling, es:

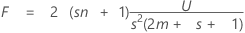
con s (2m + s + 1) y 2 (sn + 1) gl.
Notación
| Término | Description |
|---|---|
| H | matriz de hipótesis |
| E | matriz de error |
| p | número de respuestas |
| q | gl de la hipótesis |
| v | gl para E |
| s | mín (p, q) |
| m | .5 ( | p – q | – 1) |
| n | .5 (v – p – 1) |
| r | v – 0.5 (p – q + 1) |
| u | 0.25(pq – 2) |
| t | = raízcuad ([p2 q2 - 4] / p2 + q2 - 5, si p2 + q2 - 5 > 0 |
| t | 1 |
Sea λ1≥λ2≥λ3≥ . . . ≥λp siendo los valores propios de (E** - 1) * H. Los primeros tres estadísticos de prueba pueden expresarse en términos de H y E o estos valores propios.
La matriz H es una matriz p x p que contiene la suma de cuadrados "entre" en la diagonal de cada una de las variables p.. La matriz H se calcula como:

La matriz E es una matriz p x p que contiene la suma de cuadrados "dentro" en la diagonal de cada una de las variables p. La matriz E se calcula como:
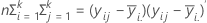
En las primeras tres pruebas, el estadístico F es exacto, si s = 1 ó 2; de lo contrario es aproximado. Minitab le dice cuando la prueba es aproximada.
Prueba de Pillai
El estadístico de prueba, el rastreo de Pillai, es:


Notación
| Término | Description |
|---|---|
| H | matriz de hipótesis |
| E | matriz de error |
| p | número de respuestas |
| q | gl de la hipótesis |
| v | gl para E |
| s | mín (p, q) |
| m | .5 ( | p – q | – 1) |
| n | .5 (v – p – 1) |
| r | v – 0.5 (p – q + 1) |
| u | 0.25(pq – 2) |
| t | = raízcuad ([p2 q2 - 4] / p2 + q2 - 5, si p2 + q2 - 5 > 0 |
| t | 1 |
Sea λ1≥λ2≥λ3≥ . . . ≥λp siendo los valores propios de (E** - 1) * H.. Los primeros tres estadísticos de prueba pueden expresarse en términos de H y E o estos valores propios.
La matriz H es una matriz p x p que contiene la suma de cuadrados "entre" en la diagonal de cada una de las variables p.. La matriz H se calcula como:

La matriz E es una matriz p x p que contiene la suma de cuadrados "dentro" en la diagonal de cada una de las variables p. La matriz E se calcula como:
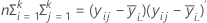
En las primeras tres pruebas, el estadístico F es exacto, si s = 1 ó 2; de lo contrario es aproximado. Minitab le dice cuando la prueba es aproximada.
Prueba de la raíz máxima de Roy
El valor propio más grande, λ1. Para terminar la prueba, se deben utilizar gráficos especiales, gráficos Heck, junto con los parámetros s, m y n, para encontrar el nivel de significancia.
Véase Heck1 para estos gráficos.
Notación
| Término | Description |
|---|---|
| s | mín (p, q) |
| m | .5 ( | p – q | – 1) |
| n | .5 (v – p – 1) |
Sea λ1≥λ2≥λ3≥ . . . ≥λp siendo los valores propios de (E** - 1) * H.. Los primeros tres estadísticos de prueba pueden expresarse en términos de H y E o estos valores propios.
- D.L. Heck (1960), "Charts of Some Upper Percentage Points of the Distribution of the Largest Characteristic Root," The Annals of Statistics, 625–642.
