Interpretar los resultados clave para MANOVA general

Utilice los análisis de valores y vectores propios para evaluar la forma cómo las medias de respuesta difieren entre los niveles de los diferentes términos del modelo. Se poner énfasis en los vectores propios que correspondan a los valores propios altos. Para mostrar los análisis de valores y vectores propios, vaya a Estadísticas > ANOVA > MANOVA general > Resultados y seleccione Análisis de valores y vectores propios en Presentación de resultados.

Utilice la tabla Medias para entender las diferencias estadísticamente significativas entre los niveles de los factores en sus datos. La media de cada grupo proporciona una estimación de cada media de población. Busque diferencias entre las medias de grupo para los términos que son estadísticamente significativos.

Para los efectos principales, la tabla muestra los grupos dentro de cada factor y sus medias. Para los efectos de interacción, la tabla muestra todas las combinaciones posibles de los grupos. Si un término de interacción es estadísticamente significativo, no interprete los efectos principales sin considerar los efectos de interacción.

Para mostrar las medias, vaya a Estadísticas > ANOVA > MANOVA general > Resultados, seleccione Análisis de univariantes de la varianza, e ingrese los términos en Mostrar las medias de los cuadrados mínimos correspondientes a los términos.

Cuando se realiza MANOVA general, se puede elegir calcular los estadísticos univariados para examinar las respuestas individuales. Los resultados univariados pueden proporcionar una comprensión más intuitiva de las relaciones en los datos. Sin embargo, los resultados univariados pueden diferir de los resultados multivariados.

Para mostrar los resultados univariados, vaya a Estadísticas > ANOVA > MANOVA general > Resultados y seleccione Análisis de univariantes de la varianza en Presentación de resultados.

Utilice las gráficas de residuos como ayuda para determinar si el modelo es adecuado y cumple con los supuestos del análisis. Si los supuestos no se cumplen, el modelo podría no ajustarse adecuadamente a los datos y se debería tener cuidado al interpretar los resultados.

Cuando se realiza el análisis MANOVA general, Minitab muestra las gráficas de residuos para todas las variables de respuesta que están en el modelo. Usted debe determinar si las gráficas de residuos para todas las variables de respuesta indican que el modelo cumple con los supuestos.

Para obtener más información sobre cómo manejar los patrones en las gráficas de residuos, vaya a Gráficas de residuos para MANOVA general y haga clic en el nombre de la gráfica de residuos en la lista que se encuentra en la parte superior de la página.

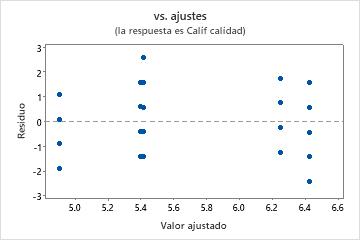
Gráfica de residuos vs. ajustes

Utilice la gráfica de residuos vs. ajustes para verificar el supuesto de que los residuos están distribuidos aleatoriamente y tienen una varianza constante. Lo ideal es que los puntos se ubiquen aleatoriamente a ambos lados del 0, con patrones no detectables en los puntos.

Los patrones que se observan en la siguiente tabla podrían indicar que el modelo no cumple con los supuestos del modelo.

Patrón	Lo que podría indicar el patrón
Dispersión en abanico o irregular de los residuos en los valores ajustados	Varianza no constante
Curvilíneo	Un término de orden superior faltante
Un punto que está alejado de cero	Un valor atípico
Un punto que está lejos de los otros puntos en la dirección x	Un punto influyente

En esta gráfica de residuos vs. ajustes, los datos parecen estar distribuidos aleatoriamente alrededor de cero. No existe evidencia de que el valor del residuo dependa del valor ajustado.

Gráfica de residuos vs. orden

Utilice la gráfica de residuos vs. orden para verificar el supuesto de que los residuos son independientes entre sí. Los residuos independientes no muestran tendencias ni patrones cuando se muestran en orden cronológico. Los patrones en los puntos podrían indicar que los residuos que están cercanos entre sí podrían estar correlacionados y, por lo tanto, podrían no ser independientes. Lo ideal es que los residuos que se muestran en la gráfica se ubiquen aleatoriamente alrededor de la línea central:

Si observa un patrón, investigue la causa. Los siguientes tipos de patrones pueden indicar que los residuos son dependientes.

Tendencia

Cambio

Ciclo

En esta gráfica de residuos vs. orden, los residuos parecen estar ubicados aleatoriamente alrededor de la línea central. No hay evidencia de que los residuos no sean independientes.

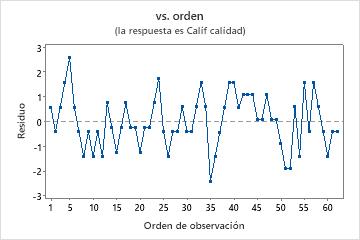
Gráfica de probabilidad normal de los residuos

Utilice la gráfica de probabilidad normal de los residuos para verificar el supuesto de que los residuos están distribuidos normalmente. La gráfica de probabilidad normal de los residuos debe seguir aproximadamente una línea recta.

Los patrones que se observan en la siguiente tabla podrían indicar que el modelo no cumple con los supuestos del modelo.

Patrón	Lo que podría indicar el patrón
No una línea recta	No normalidad
Un punto que está alejado de la línea	Un valor atípico
Pendiente cambiante	Una variable no identificada

En esta gráfica de probabilidad normal, los puntos generalmente siguen una línea recta. No hay evidencia de no normalidad, valores atípicos o variables no identificadas.