Medias
La tabla Medias muestra las medias ajustadas de las observaciones en los grupos basadas en una o más variables categóricas. Las medias ajustadas utilizan los mínimos cuadrados para predecir los valores de respuesta media de un diseño balanceado.
Interpretación
Las medias ajustadas estiman la respuesta promedio en diferentes niveles de un factor, promediando al mismo tiempo los niveles de los otros factores.
Utilice la tabla Medias para entender las diferencias estadísticamente significativas entre los niveles de los factores en sus datos. La media de cada grupo proporciona una estimación de cada media de población. Busque diferencias entre las medias de grupo para los términos que son estadísticamente significativos.
Para los efectos principales, la tabla muestra los grupos dentro de cada factor y sus medias. Para los efectos de interacción, la tabla muestra todas las combinaciones posibles de los grupos. Si un término de interacción es estadísticamente significativo, no interprete los efectos principales sin considerar los efectos de interacción.
En estos resultados, la tabla Medias muestra la variación en la media de facilidad de uso y las calificaciones de calidad según el método, la planta y la interacción método*planta. El método y el término de interacción son estadísticamente significativos en el nivel 0.10. La tabla muestra que el método 1 y el método 2 están asociados con las calificaciones medias de facilidad de uso de 4.819 y 6.212, respectivamente. La diferencia entre estas medias es mayor que la diferencia entre las medias correspondientes para la calificación de calidad. Esto confirma la interpretación de los análisis de valores y vectores propios.
Sin embargo, puesto que el término de interacción Método*Planta también es estadísticamente significativo, no interprete los efectos principales sin considerar los efectos de interacción. Por ejemplo, la tabla para el término de interacción muestra que con el método 1, la planta C está asociada con la mayor calificación de facilidad de uso y la menor calificación de calidad. Sin embargo, con el método 2, la planta A está asociada con la mayor calificación de facilidad de uso y una calificación de calidad que es casi igual a la mayor calificación de calidad.
Medias de mínimos cuadrados para Respuestas
| Calif fácil uso | Calif calidad | |||
|---|---|---|---|---|
| Media | Error estándar de la media | Media | Error estándar de la media | |
| Método | ||||
| Método 1 | 4.819 | 0.165 | 5.242 | 0.193 |
| Método 2 | 6.212 | 0.179 | 6.026 | 0.211 |
| Planta | ||||
| Planta A | 5.708 | 0.192 | 5.833 | 0.226 |
| Planta B | 5.493 | 0.232 | 5.914 | 0.273 |
| Planta C | 5.345 | 0.206 | 5.155 | 0.242 |
| Método*Planta | ||||
| Método 1 Planta A | 4.667 | 0.272 | 5.417 | 0.319 |
| Método 1 Planta B | 4.700 | 0.298 | 5.400 | 0.350 |
| Método 1 Planta C | 5.091 | 0.284 | 4.909 | 0.334 |
| Método 2 Planta A | 6.750 | 0.272 | 6.250 | 0.319 |
| Método 2 Planta B | 6.286 | 0.356 | 6.429 | 0.418 |
| Método 2 Planta C | 5.600 | 0.298 | 5.400 | 0.350 |
EE media
El error estándar de la media (EE media) estima la variabilidad entre las medias ajustadas que se obtendría si se tomaran muestras de la misma población una y otra vez.
Por ejemplo, usted tiene un tiempo de entrega medio de 3.80 días, con una desviación estándar de 1.43 días, de una muestra aleatoria de 312 tiempos de entrega. Estos números producen un error estándar de la media de 0.08 días (1.43 dividido entre la raíz cuadrada de 312). Si usted tomara múltiples muestras aleatorias del mismo tamaño y de la misma población, la desviación estándar de esas medias de muestra diferentes habría estado alrededor de 0.08 días.
Interpretación
Utilice el error estándar de la media para determinar con cuánta precisión la media ajustada estima la media de la población.
Un valor más bajo del error estándar de la media indica una estimación más precisa de la media de la población. Por lo general, una desviación estándar más grande da como resultado un mayor error estándar de la media y una estimación menos precisa de la media de la población. Un tamaño de muestra más grande da como resultado un menor error estándar de la media y una estimación más precisa de la media de la población.
Media (covariable)
La media de la covariable es el promedio de los datos, que es la suma de todas las observaciones dividida entre el número de observaciones. La media resume los valores de la muestra con un valor individual que representa el centro de los datos.
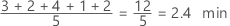
Interpretación
Utilice la media para describir la covariable con un solo valor que representa el centro de los datos.
Desviación estándar (Desv.Est.)
La desviación estándar es la medida de dispersión más común, que indica qué tan dispersos están los datos con respecto a la media. El símbolo σ (sigma) suele utilizarse para representar la desviación estándar de una población. El símbolo s se utiliza para representar la desviación estándar de una muestra.
Interpretación
- Aproximadamente un 68 % de los valores caen en una desviación estándar de la media.
- 95 % de los valores caen en dos desviaciones estándar.
- 99.7 % de los valores caen en tres desviaciones estándar.
La desviación estándar de la muestra de un grupo es una estimación de la desviación estándar de la población de ese grupo. Las desviaciones estándar se usan para calcular los intervalos de confianza y los valores p. Las desviaciones estándar más grandes se traducirán en intervalos de confianza menos precisos (más amplios) y de más baja potencia estadística.
El análisis de varianza presupone que las desviaciones estándar de la población para todos los niveles son iguales. Si no se pueden presuponer varianzas iguales, utilice ANOVA de Welch, que es una opción de ANOVA de un solo factor, disponible en Minitab Statistical Software.
