En este tema
Modelo GLM
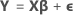
Notación
| Término | Description |
|---|---|
| Y | vector de respuestas |
| X | matriz de diseño |
| β | vector de parámetros |
| ε | vector de variables aleatorias normales independientes |
Matriz de diseño
El Modelo lineal general utiliza un método de regresión para ajustar el modelo que se especifique. Primero Minitab crea una matriz de diseño a partir de los factores y las covariables, y el modelo que usted especifique. Las columnas de esta matriz son los predictores de la regresión.
La matriz de diseño tiene n filas donde n = número de observaciones y varios bloques de columnas correspondientes a los términos en el modelo. El primer bloque se reserva para la constante y contiene sólo una columna formada por números uno. El bloque de una covariable también contiene sólo una columna, la propia columna de la covariable. El bloque de columnas para un factor contiene columnas r, donde r = grados de libertad para el factor y están codificadas como se muestra en el ejemplo a continuación.
Supongamos que A es un factor con 4 niveles. Luego, supongamos que tiene 3 grados de libertad y que su bloque contiene 3 columnas, que llamaremos A1, A2, A3.
| Nivel de A | A1 | A2 | A3 |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 |
| 4 | –1 | –1 | –1 |
Supongamos que el factor B tiene 3 niveles anidados dentro de cada nivel de A. Entonces su bloque contiene (3 - 1) x 4 = 8 columnas, las llamaremos B11, B12, B21, B22, B31, B32, B41, B42, codificadas como sigue:
| Nivel de A | Nivel de B | B11 | B12 | B21 | B22 | B31 | B32 | B41 | B42 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 3 | –1 | –1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 2 | 3 | 0 | 0 | –1 | –1 | 0 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 3 | 2 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 3 | 3 | 0 | 0 | 0 | 0 | –1 | –1 | 0 | 0 |
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 4 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | –1 | –1 |
Para calcular las columnas de un término de interacción, solo multiplique todas las columnas correspondientes por los factores o covariables en la interacción. Por ejemplo, suponga que el factor A tiene 6 niveles, C tiene 3 niveles, D tiene 4 niveles y Z y W son covariables. Entonces el término A * C * D * Z * W * W tiene 5 x 2 x 3 x 1 x 1 x 1 = 30 columnas. Para obtenerlas, multiplique cada columna de A por cada una de C, por cada una de D, por las covariables de Z una vez y las de W dos veces.
Transformación de Box-Cox
La transformación de Box Cox selecciona los valores de lambda, como se muestra a continuación, que minimizan la suma de los cuadrados de los residuos. La transformación resultante es Y λ cuando λ ≠ 0 y ln(Y) cuando λ = 0. Cuando λ < 0, Minitab también multiplica la respuesta transformada por −1 para mantener el orden de la respuesta no transformada.
Minitab busca un valor óptimo entre −2 y 2. Los valores que estén fuera de este intervalo podrían no producir un mejor ajuste.
Las siguientes son algunas transformaciones comunes donde Y′ es la transformación de los datos Y:
| Valor de lambda (λ) | Transformación |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0.5 | Y′ = 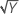 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0.5 |  |
| λ = −1 | Y′ = −1 / Y |
Regresión ponderada
La regresión de mínimos cuadrados ponderados es un método para tratar las observaciones que tienen varianzas no constantes. Si las varianzas no son constantes, a las observaciones con:
- a las grandes varianzas se les debe ofrecer ponderaciones relativamente pequeñas
- a las pequeñas varianzas se les debe ofrecer ponderaciones relativamente grandes
La elección de ponderaciones generalmente es la inversa de la varianza de error puro en la respuesta.
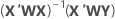
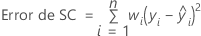
Notación
| Término | Description |
|---|---|
| X | matriz de diseño |
| X' | transpuesta de la matriz de diseño |
| W | una matriz n x n con las ponderaciones en la diagonal |
| Y | vector de valores de respuesta |
| n | número de observaciones |
| wi | ponderación de la iésima observación |
| yi | valor de respuesta de la iésima observación |
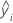 | valor ajustado de la iésima observación |
Cómo elimina Minitab los predictores muy correlacionados de la ecuación de regresión en Ajustar modelo lineal general
- Minitab realiza una descomposición QR en la matriz X.
Nota
Usar la descomposición QR para calcular el R2 es más rápido que usar la regresión de mínimos cuadrados.
- Minitab hace la regresión de un predictor sobre todos los demás predictores y calcula el valor de R2. Si 1 – R2 < 4 * 2.22e-16, entonces el predictor no pasa la prueba y es eliminado del modelo.
- Minitab repite los pasos 1 y 2 para los predictores restantes.
Ejemplo
- Minitab hace la regresión de X5 sobre X1-X4. Si 1 – R2 es mayor que 4 * 2.22e-16, entonces X5 permanece en la ecuación. X5 pasa la prueba y permanece en la ecuación.
- Minitab hace la regresión de X4 sobre X1, X2, X3 y X5. Supongamos que 1 – R2 para esta regresión es mayor que 4 * 2.22e-16 y, por lo tanto, permanece en la ecuación.
- Minitab hace la regresión de X3 sobre X1, X2, X4 y X5 y calcula el valor de R2. X3 no pasa la prueba y es eliminado de la ecuación.
- Minitab realiza una nueva descomposición QR sobre la matriz X y hace la regresión de X2 sobre los predictores restantes, X1, X4 y X5. X2 pasa la prueba.
- Minitab hace la regresión de X1 sobre X2, X4 y X5. No pasa la prueba y es eliminado de la ecuación.
Minitab hace la regresión de Y sobre X2, X4, X5. Los resultados incluyen un mensaje que indica que los predictores X1 y X3 no se pueden estimar y fueron eliminados del modelo.
Nota
Usted puede usar el subcomando TOLERANCE con el comando de sesión GLM para hacer que Minitab mantenga en el modelo un predictor que esté muy correlacionado con otro predictor. Sin embargo, bajar la tolerancia podría ser peligroso debido a la posibilidad de que se produzcan resultados numéricamente inexactos.
