Métodos y fórmulas para ANOVA balanceado

Modelo de ANOVA balanceado

El modelo de ANOVA balanceado de tres o más factores es una extensión sencilla de un análisis de dos factores del modelo de varianza,

Un modelo ANOVA balanceado de tres factores con factores A, B y C es:

y_ijkm = μ + α _i+ β _j+ γ _k + (αβ)_ij+ (αγ)_ik+ (βγ)_jk+ (αβγ)_ijk+ε_ijkm

Si los factores son fijos, Σα_i = 0, Σβ_j = 0, Σγ_k = 0, Σ(αβ)_ij = 0, Σ(αγ)_ik = 0, Σ(βγ)_jk = 0, Σ(αβγ)_ijk = 0 y ε_ijkm son independientes N(0, σ²).

Si los factores son aleatorios, α _i, β _j, γ_k, (αβ)_ij, (αγ)_ik, (βγ)_jk, (αβγ)_ijk,y ε_ijkmson variables aleatorias independientes. Las variables son distribuidas normalmente con media cero y varianzas dadas por V(α_i) = σ²_α,V(β _j) = σ²_β,V(γ_k) = σ²_γ, V[(αβ)_ij] = σ²_αβ, V[(αγ)_jk] = σ²_αγ, V[(βγ)_jk] = σ²_βγ, V(ε_ijkm) = σ².

El modelo de tres factores puede extenderse a modelos con más de tres factores.

Medias de factor

Fórmula

El promedio de las observaciones para un factor a un nivel de factor determinado. Las fórmulas son:

Media del Factor A: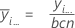

Media del factor B:

Media del Factor C: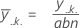

Media general:

Notación

Término	Description
y_i...	la suma de todas las observaciones para el i^ésimo nivel del factor de A
y_.j..	la suma de todas las observaciones para el j^ésimo nivel del factor de B
y_..k.	la suma de todas las observaciones para el k^ésimo nivel del factor de C
y_....	la suma de todas las observaciones en la muestra
a	número de niveles en A
b	número de niveles en B
c	número de niveles en C
n	número de observaciones en cada combinación del factor y los niveles

Suma de los cuadrados (SC)

La suma de distancias cuadradas. La SC Total es la variación total en los datos. SC (A), SC (B) y SC (C) representan la cantidad de variación alrededor de la media general. También se les conoce como la suma de los cuadrados entre los tratamientos. SC(AB), SC(AC), SC(BC) y SC(ABC) representa la cantidad de variación explicada por cada término de interacción respectivo. El error de SC representa la cantidad de variación entre el valor ajustado y la observación real. Esto se conoce también como un error en los tratamientos. Estas fórmulas asumen un modelo completo que está ajustado. Los cálculos son:

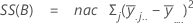
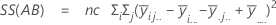
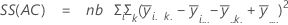
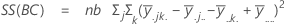
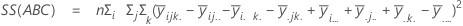
SC error = SC total - SC (para todos los términos en el modelo)

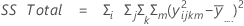
Notación

Término	Description
a	número de niveles en el factor A
b	número de niveles en el factor B
c	número de niveles en el factor C
n	Número total de ensayos
	media del i^ésimo nivel de factor del factor A
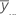	media general de todas las observaciones
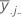	media del j^ésimo nivel de factor del factor B
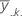	media del j^ésimo nivel de factor del factor C
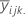	media de tratamiento estimada

Grados de libertad (GL)

Los grados de libertad para cada componente del modelo son:

Fuentes de variación	GL
Factor	k_i – 1
Covariables e interacciones entre covariables	1
Interacciones que implican factores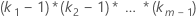
Regresión	p
Error	n – p – 1
Total	n – 1

Notación

Término	Description
k_i	número de niveles en el i^ésimo factor
m	número de factores
n	número de observaciones
p	número de coeficientes en el modelo, sin contar la constante

Cuadrado medio (CM)

Fórmulas

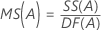
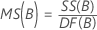
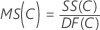
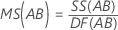
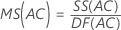
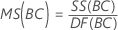
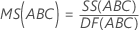
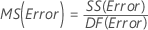
F

Para un ANOVA de 3 factores con todos los factores fijos, estas fórmulas son los estadísticos F cuando el modelo está completo.

Fórmulas

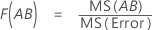
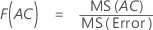
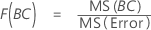
Para F(A), los grados de libertad del numerador son a - 1 y del denominador son (n - 1)abc.
Para F(B), los grados de libertad del numerador son b - 1 y del denominador son (n - 1)abc.
Para F(C), los grados de libertad del numerador son c - 1 y del denominador son (n - 1)abc.
Para F(AB), los grados de libertad del numerador son (a - 1)(b - 1) y del denominador son (n - 1)abc.
Para F(AC), los grados de libertad del numerador son (a - 1)(c - 1) y del denominador son (n - 1)abc.
Para F(BC), los grados de libertad del numerador son (b - 1)(c - 1) y del denominador son (n - 1)abc.
Para F(ABC), los grados de libertad del numerador son (a - 1)(b - 1)(c - 1) y del denominador son (n - 1)abc.

Si hay factores aleatorios en el modelo, la relación F de cada término se determina mediante el cuadrado medio esperado de cada término.

Valores elevados de F apoyan el rechazo de la hipótesis nula. Se puede concluir que el efecto es estadísticamente significativo.

Valor p – Tabla Análisis de varianza

El valor p es una probabilidad que se calcula a partir de una distribución F con los grados de libertad (GL) que se indican a continuación:

GL del numerador: suma de los grados de libertad para el término o los términos en la prueba
GL del denominador: grados de libertad para el error

Fórmula

1 − P(F ≤ f_j)

Notación

Término	Description
P(F ≤ f)	función de distribución acumulada para la distribución F
f	estadístico F para la prueba

S

Notación

Término	Description
MSE	cuadrado medio del error

R-cuad.

El R² también es denominado como el coeficiente de determinación.

Fórmula

Notación

Término	Description
y_i	i ^ésimo valor de respuesta observado
	respuesta media
	i ^iésima respuesta ajustada

R-cuad.(ajustado)

Mientras que los cálculos de R² ajustados pueden producir valores negativos, Minitab muestra el cero para estos casos.

Notación

Término	Description
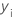	i^ésimo valor de respuesta observado
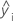	i^ésima respuesta ajustada
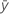	respuesta media
n	número de observaciones
p	número de términos en el modelo

Componentes de la varianza

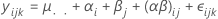
Minitab calcula los componentes de varianza solamente para los factores aleatorios. Se usa un modelo con dos factores aleatorios para presentar las fórmulas.

donde, α_i, β_j, (αβ)_ij, y ε_ijk son variables aleatorias independientes. Las variables normalmente están distribuidas con cero media y varianzas dadas por estas fórmulas:

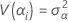
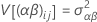
Estas varianzas son los componentes de varianza. En este caso, se prueba la hipótesis de que los componentes de varianza son iguales a cero.

Para un modelo mixto restringido con dos factores, el modelo es:

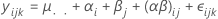
donde α_i es un efecto fijo y β_j es un efecto aleatorio, (αβ)_ij, es un efecto aleatorio, y ε_ijk es un error aleatorio. La Σα_i = 0 y la Σ(αβ)_ij = 0 para cada j. Las varianzas son V(β_j) = σ²_β,V[(αβ)_ij] =[(a - 1)/a]σ²_αβ, y V(ε_ijk) = σ². σ²_β, σ²_αβ, y σ² son componentes de varianza. En resumen el componente de interacción sobre el factor fijo es igual a cero, lo que indica que este es el modelo mixto restringido.

Para un modelo mixto no restringido con un factor fijo, A, y un factor aleatorio, B, esta fórmula describe el modelo:

donde α_i son efectos fijos y β_j, (αβ)_ij y ε_ijk son variables aleatorias no relacionadas que tienen medias de cero y estas varianzas:

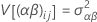
Estas varianzas son los componentes de varianza. La Σα i = 0 y Σ(αβ)ij = 0 para cada j.

Esta información es para modelos balanceados. Para información sobre modelos más complejos o no balanceados, véase Montgomery¹ y Neter².

D.C. Montgomery (1991). Design and Analysis of Experiments, Third Edition. John Wiley & Sons.
J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.

Cuadrados medios esperados

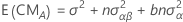
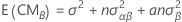
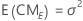
Las fórmulas de los cuadrados medios esperados para un modelo de efectos aleatorios con dos factores, A y B son:

Las fórmulas de los cuadrados medios esperados para un modelo mixto restringido con dos factores, A (fijo) y B (aleatorio) son:

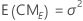
Las fórmulas de los cuadrados medios esperados para un modelo mixto sin restricciones con un factor fijo, A, y un factor aleatorio, B, son:

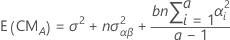
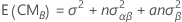
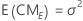
Para las reglas sobre como calcular los cuadrados medios esperados y para información sobre modelos más complejos o no balanceados, véase Montgomery¹ y Neter².

D.C. Montgomery (1991). Design and Analysis of Experiments, Third Edition. John Wiley & Sons.
J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, Second Edition. Irwin, Inc.

Notación

Término	Description
b	número de niveles en el factor B
a	número de niveles en el factor A
n	número de observaciones
σ²	varianza estimada del modelo
	varianza estimada de A
	varianza estimada de B
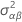	varianza estimada de AB
	efectos fijos de A

Estadístico F para modelos con factores aleatorios

Cómo se calculan los estadísticos F en la salida de ANOVA

Cada estadístico F es una relación de cuadrados medios. El numerador es el cuadrado medio del término. El denominador se escoge de manera que el valor esperado del cuadrado medio del numerador difiera del valor esperado del cuadrado medio del denominador solo por el efecto de interés. El efecto de un término aleatorio está representado por el componente de la varianza del término. El efecto de un término fijo está representado por la suma de los cuadrados de los componentes del modelo asociados con ese término dividida entre sus grados de libertad. Por lo tanto, un estadístico F alto indica un efecto significativo.

Cuando todos los términos del modelo son fijos, el denominador para cada estadístico F es el cuadrado medio del error (MSE). Sin embargo, para los modelos que incluyen términos aleatorios, el MSE no siempre es el cuadrado medio correcto. Los cuadrados medios esperados (EMS) pueden utilizarse para determinar qué es lo apropiado para el denominador.

Ejemplo

Supongamos que usted realizó un ANOVA con el factor fijo Pantalla y el factor aleatorio Tecno y obtiene la siguiente salida para el EMS:

Fuente	Cuadrado medio esperado para cada término
(1) Pantalla	(4) + 2.00(3) + Q[1]
(2) Tecno	(4) + 2,0000(3) + 4,0000(2)
(3) Pantalla*Tecno	(4) + 2,0000(3)
(4) Error	(4)

Un número entre paréntesis indica un efecto aleatorio asociado con el término que aparece al lado del número de la fuente. (2) representa el efecto aleatorio de Tecno, (3) representa el efecto aleatorio de la interacción Pantalla*Tecno y (4) representa el efecto aleatorio del Error. El EMS para Error es el efecto del término de error. Además, el EMS para Pantalla*Tecno es el efecto del término de error más dos veces el efecto de la interacción Pantalla*Tecno.

Para calcular el estadístico F de Pantalla*Tecno, el cuadrado medio de Pantalla*Tecno se divide entre el cuadrado medio del error de modo que el valor esperado del numerador (EMS para Pantalla*Tecno = (4) + 2.00(3)) difiera del valor esperado del denominador (EMS para Error = (4)) solo por el efecto de la interacción (2.00(3)). Por lo tanto, un estadístico F alto indica una interacción Pantalla*Tecno significativa.

Un número con Q[ ] indica el efecto fijo asociado con el término que aparece al lado del número de la fuente. Por ejemplo, Q[1] es el efecto fijo de Pantalla. El EMS para Pantalla es el efecto del término de error más dos veces el efecto de la interacción Pantalla*Tecno más una constante multiplicada por el efecto de Pantalla. Q[1] es igual a (b*n * suma((coeficientes de los niveles de Pantalla)**2)) dividido entre (a - 1), donde a y b son el número de niveles de Pantalla y Tecno, respectivamente, y n es el número de réplicas.

Para calcular el estadístico F para Pantalla, el cuadrado medio de Pantalla se divide entre el cuadrado medio de Pantalla*Tecno de modo que el valor esperado del numerador (EMS para Pantalla = (4) + 2.0000(3) + Q[1]) difiera del valor esperado del denominador (EMS para Pantalla*Tecno = (4) + 2.0000(3) ) solo por el efecto debido a la Pantalla (Q[1]). Por lo tanto, un estadístico F alto indica un efecto significativo de Pantalla.

¿Por qué incluye la salida de mi ANOVA una "x" al lado del valor p en la tabla ANOVA y la etiqueta "No es una prueba F exacta"?

Una prueba F exacta para un término es aquella en la que el valor esperado de los cuadrados medios del numerador difiere del valor esperado de los cuadrados medios del denominador solo por el componente de la varianza o el factor fijo de interés.

Sin embargo, a veces no es posible calcular ese cuadrado medio. En ese caso, Minitab utiliza un cuadrado medio que da como resultado una prueba F aproximada y muestra una "x" al lado el valor p para indicar que la prueba F no es exacta.

Por ejemplo, supongamos que usted realizó un ANOVA con el factor fijo Suplemento y el factor aleatorio Lago y obtuvo la siguiente salida para los cuadrados medios esperados (EMS):

Fuente	Cuadrado medio esperado para cada término
(1) Suplemento	(4) + 1,7500(3) + Q[1]
(2) Lago	(4) + 1,7143(3) + 5,1429(2)
(3) Suplemento*Lago	(4) + 1,7500(3)
(4) Error	(4)

El estadístico F para Suplemento es el cuadrado medio de Suplemento dividido entre el cuadrado medio de la interacción Suplemento*Lago. Si el efecto para Suplemento es muy pequeño, el valor esperado del numerador es igual al valor esperado del denominador. Este es un ejemplo de una prueba F exacta.

Sin embargo, observe que para un efecto muy pequeño de Lago no hay cuadrados medios tales que el valor esperado del numerador sea igual al valor esperado del denominador. Por lo tanto, Minitab utiliza una prueba F aproximada. En este ejemplo, el cuadrado medio de Lago se divide entre el cuadrado medio de la interacción Suplemento*Lago. Esto da como resultado un valor esperado del numerador que es aproximadamente igual al del denominador si el efecto de Lago es muy pequeño.

Acerca del mensaje "El denominador de la prueba F es cero o no está definido"

Minitab mostrará un mensaje de error indicando que el denominador de la prueba F es cero o no está definido, por una de las siguientes razones:

No hay al menos un grado de libertad para el error.
Los valores ajustados de CM son muy pequeños y por lo tanto no hay suficiente precisión para mostrar los valores p y F. Como una solución, multiplique la columna de respuesta por 10. Entonces ejecute el mismo modelo de regresión, pero en cambio utilice esta nueva columna de respuesta para la respuesta.

Nota
Multiplicar los valores de respuesta por 10 no afectará los valores F y p que Minitab muestra en la salida. Sin embargo, la posición decimal se verá afectada en la salida restante, específicamente, las sumas secuenciales de los cuadrados, SC Ajust., CM Ajust., Ajuste, error estándar de los ajustes y las columnas de residuos.

Cómo se calculan los estadísticos F en la salida de ANOVA

Cada estadístico F es una relación de cuadrados medios. El numerador es el cuadrado medio del término. El denominador se escoge de manera que el valor esperado del cuadrado medio del numerador difiera del valor esperado del cuadrado medio del denominador solo por el efecto de interés. El efecto de un término aleatorio está representado por el componente de la varianza del término. El efecto de un término fijo está representado por la suma de los cuadrados de los componentes del modelo asociados con ese término dividida entre sus grados de libertad. Por lo tanto, un estadístico F alto indica un efecto significativo.

Cuando todos los términos del modelo son fijos, el denominador para cada estadístico F es el cuadrado medio del error (MSE). Sin embargo, para los modelos que incluyen términos aleatorios, el MSE no siempre es el cuadrado medio correcto. Los cuadrados medios esperados (EMS) pueden utilizarse para determinar qué es lo apropiado para el denominador.

Ejemplo

Supongamos que usted realizó un ANOVA con el factor fijo Pantalla y el factor aleatorio Tecno y obtiene la siguiente salida para el EMS:

Fuente	Cuadrado medio esperado para cada término
(1) Pantalla	(4) + 2.00(3) + Q[1]
(2) Tecno	(4) + 2,0000(3) + 4,0000(2)
(3) Pantalla*Tecno	(4) + 2,0000(3)
(4) Error	(4)

Un número entre paréntesis indica un efecto aleatorio asociado con el término que aparece al lado del número de la fuente. (2) representa el efecto aleatorio de Tecno, (3) representa el efecto aleatorio de la interacción Pantalla*Tecno y (4) representa el efecto aleatorio del Error. El EMS para Error es el efecto del término de error. Además, el EMS para Pantalla*Tecno es el efecto del término de error más dos veces el efecto de la interacción Pantalla*Tecno.

Para calcular el estadístico F de Pantalla*Tecno, el cuadrado medio de Pantalla*Tecno se divide entre el cuadrado medio del error de modo que el valor esperado del numerador (EMS para Pantalla*Tecno = (4) + 2.00(3)) difiera del valor esperado del denominador (EMS para Error = (4)) solo por el efecto de la interacción (2.00(3)). Por lo tanto, un estadístico F alto indica una interacción Pantalla*Tecno significativa.

Un número con Q[ ] indica el efecto fijo asociado con el término que aparece al lado del número de la fuente. Por ejemplo, Q[1] es el efecto fijo de Pantalla. El EMS para Pantalla es el efecto del término de error más dos veces el efecto de la interacción Pantalla*Tecno más una constante multiplicada por el efecto de Pantalla. Q[1] es igual a (b*n * suma((coeficientes de los niveles de Pantalla)**2)) dividido entre (a - 1), donde a y b son el número de niveles de Pantalla y Tecno, respectivamente, y n es el número de réplicas.

Para calcular el estadístico F para Pantalla, el cuadrado medio de Pantalla se divide entre el cuadrado medio de Pantalla*Tecno de modo que el valor esperado del numerador (EMS para Pantalla = (4) + 2.0000(3) + Q[1]) difiera del valor esperado del denominador (EMS para Pantalla*Tecno = (4) + 2.0000(3) ) solo por el efecto debido a la Pantalla (Q[1]). Por lo tanto, un estadístico F alto indica un efecto significativo de Pantalla.

¿Por qué incluye la salida de mi ANOVA una "x" al lado del valor p en la tabla ANOVA y la etiqueta "No es una prueba F exacta"?

Una prueba F exacta para un término es aquella en la que el valor esperado de los cuadrados medios del numerador difiere del valor esperado de los cuadrados medios del denominador solo por el componente de la varianza o el factor fijo de interés.

Sin embargo, a veces no es posible calcular ese cuadrado medio. En ese caso, Minitab utiliza un cuadrado medio que da como resultado una prueba F aproximada y muestra una "x" al lado el valor p para indicar que la prueba F no es exacta.

Por ejemplo, supongamos que usted realizó un ANOVA con el factor fijo Suplemento y el factor aleatorio Lago y obtuvo la siguiente salida para los cuadrados medios esperados (EMS):

Fuente	Cuadrado medio esperado para cada término
(1) Suplemento	(4) + 1,7500(3) + Q[1]
(2) Lago	(4) + 1,7143(3) + 5,1429(2)
(3) Suplemento*Lago	(4) + 1,7500(3)
(4) Error	(4)

El estadístico F para Suplemento es el cuadrado medio de Suplemento dividido entre el cuadrado medio de la interacción Suplemento*Lago. Si el efecto para Suplemento es muy pequeño, el valor esperado del numerador es igual al valor esperado del denominador. Este es un ejemplo de una prueba F exacta.

Sin embargo, observe que para un efecto muy pequeño de Lago no hay cuadrados medios tales que el valor esperado del numerador sea igual al valor esperado del denominador. Por lo tanto, Minitab utiliza una prueba F aproximada. En este ejemplo, el cuadrado medio de Lago se divide entre el cuadrado medio de la interacción Suplemento*Lago. Esto da como resultado un valor esperado del numerador que es aproximadamente igual al del denominador si el efecto de Lago es muy pequeño.

Acerca del mensaje "El denominador de la prueba F es cero o no está definido"

Minitab mostrará un mensaje de error indicando que el denominador de la prueba F es cero o no está definido, por una de las siguientes razones:

No hay al menos un grado de libertad para el error.
Los valores ajustados de CM son muy pequeños y por lo tanto no hay suficiente precisión para mostrar los valores p y F. Como una solución, multiplique la columna de respuesta por 10. Entonces ejecute el mismo modelo de regresión, pero en cambio utilice esta nueva columna de respuesta para la respuesta.

Nota
Multiplicar los valores de respuesta por 10 no afectará los valores F y p que Minitab muestra en la salida. Sin embargo, la posición decimal se verá afectada en la salida restante, específicamente, las sumas secuenciales de los cuadrados, SC Ajust., CM Ajust., Ajuste, error estándar de los ajustes y las columnas de residuos.

Valor ajustado

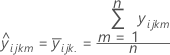
Notación

Para un modelo de 3 factores:

Término	Description
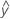	el valor ajustado para la observación en el i^ésimo nivel del factor A, el j^ésimo nivel del factor B, el k^ésimo nivel del factor C
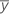	el valor medio para la observación en el i^ésimo nivel del factor A, el j^ésimo nivel del factor B, el k^ésimo nivel del factor C
n	el número de observaciones en el i^ésimo nivel del factor A, el j^ésimo nivel del factor B, el k^ésimo nivel del factor C

Residuo (Resid.)

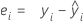
Notación

Término	Description
e_i	i ^ésimo residuo
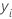	i ^ésimo valor de respuesta observado
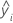	i ^iésima respuesta ajustada

Métodos y fórmulas para ANOVA balanceado

En este tema

Modelo de ANOVA balanceado

Medias de factor

Fórmula

Notación

Suma de los cuadrados (SC)

Notación

Grados de libertad (GL)

Notación

Cuadrado medio (CM)

Fórmulas

F

Fórmulas

Valor p – Tabla Análisis de varianza

Fórmula

Notación

S

Notación

R-cuad.

Fórmula

Notación

R-cuad.(ajustado)

Notación

Componentes de la varianza

Cuadrados medios esperados

Notación

Estadístico F para modelos con factores aleatorios

Cómo se calculan los estadísticos F en la salida de ANOVA

Ejemplo

¿Por qué incluye la salida de mi ANOVA una "x" al lado del valor p en la tabla ANOVA y la etiqueta "No es una prueba F exacta"?

Acerca del mensaje "El denominador de la prueba F es cero o no está definido"

Nota

Cómo se calculan los estadísticos F en la salida de ANOVA

Ejemplo

¿Por qué incluye la salida de mi ANOVA una "x" al lado del valor p en la tabla ANOVA y la etiqueta "No es una prueba F exacta"?

Acerca del mensaje "El denominador de la prueba F es cero o no está definido"

Nota

Valor ajustado

Notación

Residuo (Resid.)

Notación