En este tema
Paso 1: Determinar si la asociación entre la respuesta y el término es estadísticamente significativa
- Valor p ≤ α: La asociación es estadísticamente significativa
- Si el valor p es menor que o igual al nivel de significancia, usted puede concluir que hay una asociación estadísticamente significativa entre la variable de respuesta y el término.
- Valor p > α: La asociación no es estadísticamente significativa
- Si el valor p es mayor que el nivel de significancia, usted no puede concluir que existe una asociación estadísticamente significativa entre la variable de respuesta y el término. Convendría que vuelva a ajustar el modelo sin el término.
- Si un factor fijo es significativo, usted puede concluir que no todas las medias de nivel son iguales.
- Si un factor aleatorio es significativo, puede concluir que el factor contribuye a la cantidad de variación en la respuesta.
- Si un término de interacción es significativo, la relación entre un factor y la respuesta depende del resto de los factores incluidos en el término. En este caso, usted no debe interpretar los efectos principales sin considerar el efecto de interacción.
Utilice la tabla Medias para entender las diferencias estadísticamente significativas entre los niveles de los factores en sus datos. La media de cada grupo proporciona una estimación de cada media de población. Busque diferencias entre las medias de grupo para los términos que son estadísticamente significativos.
Para los efectos principales, la tabla muestra los grupos dentro de cada factor y sus medias. Para los efectos de interacción, la tabla muestra todas las combinaciones posibles de los grupos. Si un término de interacción es estadísticamente significativo, no interprete los efectos principales sin considerar los efectos de interacción.
Información del factor
| Factor | Tipo | Niveles | Valores |
|---|---|---|---|
| Tiempo | Fijo | 2 | 1, 2 |
| Operador | Aleatorio | 3 | 1, 2, 3 |
| Posición | Fijo | 3 | 35, 44, 52 |
Análisis de varianza de Grosor
| Fuente | GL | SC | MC | F | P | |
|---|---|---|---|---|---|---|
| Tiempo | 1 | 9.0 | 9.00 | 0.29 | 0.644 | |
| Operador | 2 | 1120.9 | 560.44 | 4.28 | 0.081 | x |
| Posición | 2 | 15676.4 | 7838.19 | 73.18 | 0.001 | |
| Tiempo*Operador | 2 | 62.0 | 31.00 | 4.34 | 0.026 | |
| Tiempo*Posición | 2 | 114.5 | 57.25 | 8.02 | 0.002 | |
| Operador*Posición | 4 | 428.4 | 107.11 | 15.01 | 0.000 | |
| Error | 22 | 157.0 | 7.14 | |||
| Total | 35 | 17568.2 |
Resumen del modelo
| S | R-cuadrado | R-cuadrado(ajustado) |
|---|---|---|
| 2.67140 | 99.11% | 98.58% |
Términos de error para pruebas
| Fuente | Componente de la varianza | Término de error | Media de cuadrados esperada para cada término (usando el modelo no restringido) | |
|---|---|---|---|---|
| 1 | Tiempo | 4 | (7) + 6 (4) + Q[1, 5] | |
| 2 | Operador | 35.789 | * | (7) + 4 (6) + 6 (4) + 12 (2) |
| 3 | Posición | 6 | (7) + 4 (6) + Q[3, 5] | |
| 4 | Tiempo*Operador | 3.977 | 7 | (7) + 6 (4) |
| 5 | Tiempo*Posición | 7 | (7) + Q[5] | |
| 6 | Operador*Posición | 24.994 | 7 | (7) + 4 (6) |
| 7 | Error | 7.136 | (7) |
Términos de error para pruebas sintetizadas
| Fuente | GL de error | MC de error | Síntesis de MC de error | |
|---|---|---|---|---|
| 2 | Operador | 5.12 | 130.9747 | (4) + (6) - (7) |
Medias
| Tiempo | N | Grosor |
|---|---|---|
| 1 | 18 | 67.7222 |
| 2 | 18 | 68.7222 |
| Posición | N | Grosor |
|---|---|---|
| 35 | 12 | 40.5833 |
| 44 | 12 | 73.0833 |
| 52 | 12 | 91.0000 |
| Tiempo*Posición | N | Grosor |
|---|---|---|
| 1 35 | 6 | 40.6667 |
| 1 44 | 6 | 70.1667 |
| 1 52 | 6 | 92.3333 |
| 2 35 | 6 | 40.5000 |
| 2 44 | 6 | 76.0000 |
| 2 52 | 6 | 89.6667 |
Resultados clave: Valor p, tabla Medias
La configuración es un factor fijo y este efecto principal es significativo. Este resultado indica que la media del grosor del recubrimiento no es igual para todas las configuraciones de máquina.
Hora*Configuración es un efecto de interacción que implica dos factores fijos. Este efecto de interacción es significativo, lo cual indica que la relación entre cada factor y la respuesta depende del nivel del otro factor. En este caso, no se deben interpretar los efectos principales sin considerar el efecto de interacción.
En estos resultados, la tabla Medias muestra la variación en la media de grosor según el tiempo, la configuración de la máquina y cada combinación de tiempo y configuración de la máquina. El valor de configuración es estadísticamente significativo y las medias difieren entre las configuraciones de la máquina. Sin embargo, puesto que el término de interacción Tiempo*Configuración también es estadísticamente significativo, no interprete los efectos principales sin considerar los efectos de interacción. Por ejemplo, la tabla para el término de interacción muestra que con una configuración de 44, el tiempo 2 está asociado con un recubrimiento más grueso. Sin embargo, con una configuración de 52, el tiempo 1 está asociado con un recubrimiento más grueso.
El operador es un factor aleatorio y todas las interacciones que incluyen un factor aleatorio son consideradas aleatorias. Si un factor aleatorio es significativo, se puede concluir que el factor contribuye a la cantidad de variación en la respuesta. El operador no es significativo al nivel de 0.05, pero los efectos de interacción que incluye el operador son significativos. Estos efectos de interacción indican que la cantidad de variación con la que el operador contribuye a la respuesta depende del valor tanto de hora como configuración de máquina.
Paso 2: Determinar hasta qué punto el modelo se ajusta a los datos
Para determinar qué tan bien se ajusta el modelo a los datos, examine los estadísticos de bondad de ajuste en la tabla Resumen del modelo.
- S
-
Utilice S para evaluar qué tan bien el modelo describe la respuesta. Utilice S en lugar de los estadísticos R2 para comparar el ajuste de los modelos que no tienen una constante.
S se mide en las unidades de la variable de respuesta y representa la distancia que separa a los valores de los datos de los valores ajustados. Mientras más bajo sea el valor de S, mejor describirá el modelo la respuesta. Sin embargo, un valor de S bajo no indica por sí solo que el modelo cumple con los supuestos del modelo. Debe examinar las gráficas de residuos para verificar los supuestos.
- R-cuad.
-
Mientras mayor sea el valor de R2, mejor se ajustará el modelo a los datos. R2 siempre está entre 0% y 100%.
El R2 siempre se incrementa cuando usted agrega predictores adicionales a un modelo. Por ejemplo, el mejor modelo de cinco predictores siempre tendrá un R2 que será al menos tan alto como el mejor modelo de cuatro predictores. Por lo tanto, R2 es más útil cuando se comparan modelos del mismo tamaño.
- R-cuad.(ajustado)
-
Utilice R2 ajustado cuando desee comparar modelos que tengan diferentes números de predictores. R2 siempre aumenta cuando se agrega un predictor al modelo, incluso cuando no haya una mejora real en el modelo. El valor de R2 ajustado incorpora el número de predictores del modelo para ayudar a elegir el modelo correcto.
-
Las muestras pequeñas no proporcionan una estimación precisa de la fuerza de la relación entre la respuesta y los predictores. Por ejemplo, si necesita que R2 sea más preciso, debe utilizar una muestra más grande (generalmente, 40 o más).
-
Los estadísticos de bondad de ajuste son simplemente una medida de qué tan bien se ajusta el modelo a los datos. Incluso cuando un modelo tenga un valor deseable, usted deberá revisar las gráficas de residuos para verificar que el modelo cumpla con los supuestos del modelo.
Resumen del modelo
| S | R-cuadrado | R-cuadrado(ajustado) |
|---|---|---|
| 2.67140 | 99.11% | 98.58% |
Resultados clave: S, R-cuad., R-cuad. (ajust)
En estos resultados, el modelo explica un 99.11 % de la variación en el grosor del recubrimiento. Para estos datos, el valor de R2 indica el modelo que ofrece un mejor ajuste para los datos. Si se ajustan modelos adicionales con diferentes predictores, utilice los valores de R2 ajustados para comparar hasta que punto el modelo se ajusta a los datos.
Paso 3: Determinar si el modelo cumple con los supuestos del análisis
Utilice las gráficas de residuos como ayuda para determinar si el modelo es adecuado y cumple con los supuestos del análisis. Si los supuestos no se cumplen, el modelo podría no ajustarse adecuadamente a los datos y se debería tener cuidado al interpretar los resultados.
Para obtener más información sobre cómo manejar los patrones en las gráficas de residuos, vaya a Gráficas de residuos para Ajustar modelo lineal general y haga clic en el nombre de la gráfica de residuos en la lista que se encuentra en la parte superior de la página.
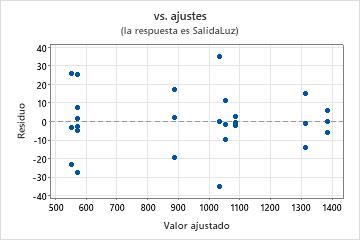
Gráfica de residuos vs. ajustes
Utilice la gráfica de residuos vs. ajustes para verificar el supuesto de que los residuos están distribuidos aleatoriamente y tienen una varianza constante. Lo ideal es que los puntos se ubiquen aleatoriamente a ambos lados del 0, con patrones no detectables en los puntos.
| Patrón | Lo que podría indicar el patrón |
|---|---|
| Dispersión en abanico o irregular de los residuos en los valores ajustados | Varianza no constante |
| Curvilíneo | Un término de orden superior faltante |
| Un punto que está alejado de cero | Un valor atípico |
| Un punto que está lejos de los otros puntos en la dirección x | Un punto influyente |
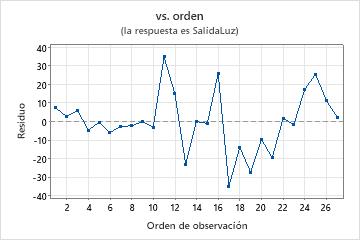
Gráfica de residuos vs. orden
Tendencia
Cambio
Ciclo
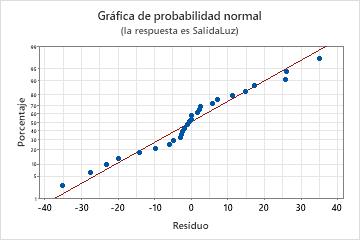
Gráfica de probabilidad normal
Utilice la gráfica de probabilidad normal de los residuos para verificar el supuesto de que los residuos están distribuidos normalmente. La gráfica de probabilidad normal de los residuos debe seguir aproximadamente una línea recta.
| Patrón | Lo que podría indicar el patrón |
|---|---|
| No una línea recta | No normalidad |
| Un punto que está alejado de la línea | Un valor atípico |
| Pendiente cambiante | Una variable no identificada |