Tabla Resumen del modelo para ANOVA balanceado

Encuentre definiciones e interpretaciones para cada estadístico en la tabla Resumen del modelo.

En este tema

S
R-cuad.
R-cuad. (ajust)

S

S representa la desviación estándar de la distancia entre los valores de datos y los valores ajustados. S se mide en las unidades de la respuesta.

Interpretación

Utilice S para evaluar qué tan bien el modelo describe la respuesta. S se mide en las unidades de la variable de respuesta y representa la distancia que separa a los valores de los datos de los valores ajustados. Mientras más bajo sea el valor de S, mejor describirá el modelo la respuesta. Sin embargo, un valor de S bajo no indica por sí solo que el modelo cumple con los supuestos del modelo. Debe examinar las gráficas de residuos para verificar los supuestos.

Por ejemplo, usted trabaja para una compañía de chips de patatas que examina los factores que afectan el número de chips desmenuzados por contenedor. Usted reduce el modelo a los predictores significativos y determina que S se calcula como 1.79. Este resultado indica que la desviación estándar de los puntos de datos alrededor de los valores ajustados es 1.79. Si está comparando modelos, los valores que son menores de 1.79 indican un mejor ajuste y los valores mayores indican un peor ajuste.

R-cuad.

R2 es el porcentaje de variación en la respuesta que se explica por el modelo. Se calcula como 1 menos la relación de la suma de los cuadrados del error (que es la variación que no es explicada por el modelo) a la suma total de los cuadrados (que es la variación total en el modelo).

Interpretación

Utilice el R² para determinar qué tan bien se ajusta el modelo a los datos Mientras mayor sea el valor de R², mejor se ajustará el modelo a los datos. R2 siempre está entre 0% y 100%.

Usted puede utilizar una gráfica de línea ajustada para ilustrar gráficamente diferentes valores de R². La primera gráfica ilustra un modelo de regresión simple que explica un 85.5% de la variación en la respuesta. La segunda gráfica ilustra un modelo que explica un 22.6% de la variación en la respuesta. Mientras mayor sea la variable que es explicada por el modelo, más cerca estarán los puntos de los datos de la línea de regresión ajustada. Teóricamente, si un modelo pudiera explicar el 100% de la variación, los valores ajustados siempre serían iguales a los valores observados y todos los puntos de los datos estarían sobre la línea ajustada. Sin embargo, incluso si el R² es 100%, el modelo no necesariamente predice las nuevas observaciones de manera adecuada.

Tenga en cuenta los siguientes problemas al interpretar el valor R2:

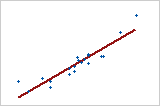
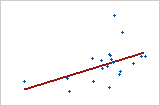
R² siempre aumenta cuando se agregan más predictores a un modelo. Por ejemplo, el mejor modelo de cinco predictores siempre tendrá un R² que será al menos tan alto como el mejor modelo de cuatro predictores. Por lo tanto, R² es más útil cuando se comparan modelos del mismo tamaño.
Las muestras pequeñas no proporcionan una estimación precisa de la fuerza de la relación entre la respuesta y los predictores. Por ejemplo, si necesita que R² sea más preciso, debe utilizar una muestra más grande (generalmente, 40 o más).
Los estadísticos de bondad de ajuste son simplemente una medida de qué tan bien se ajusta el modelo a los datos. Incluso cuando un modelo tenga un valor deseable, usted deberá revisar las gráficas de residuos para verificar que el modelo cumpla con los supuestos del modelo.

R-cuad. (ajust)

El R² ajustado es el porcentaje de la variación en la respuesta que es explicada por el modelo, ajustado para el número de predictores en el modelo relativo al número de observaciones. El R² ajustado se calcula como 1 menos la relación del cuadrado medio del error (MSE) con el cuadrado medio total (CM Total).

Interpretación

Utilice R² ajustado cuando desee comparar modelos que tengan diferentes números de predictores. R² siempre aumenta cuando se agrega un predictor al modelo, incluso cuando no haya una mejora real en el modelo. El valor de R² ajustado incorpora el número de predictores del modelo para ayudar a elegir el modelo correcto.

Por ejemplo, usted trabaja para una compañía de chips de patatas que examina los factores que afectan el número de chips desmenuzados por contenedor. Obtiene los siguientes resultados a medida que agrega los predictores de forma escalonada hacia delante.

Modelo	% Patata	Tasa de enfriamiento	Temp. de cocción	R²	R² ajustado
1	X			52	=
1	X	X		63	62
3	X	X	X	=	=

El primer modelo produce un R² de más de 50%. El segundo modelo agrega una tasa de enfriamiento al modelo. El R² ajustado se incrementa, lo cual indica que la tasa de enfriamiento mejora el modelo. El tercer modelo, que agrega un temperatura de cocción, aumenta el R² pero no el R² ajustado. Estos resultados indican que la temperatura de cocción no mejora el modelo. Con base en estos resultados, considere eliminar la temperatura de cocción del modelo.