En este tema
Método
Para los modelos de dos factores, el análisis de medias es un procedimiento para determinar si los efectos de interacción son significativos o si los efectos principales son diferentes de la media principal. Para los análisis de medias de dos factores, los datos deben estar balanceados.
Media
Fórmula
El promedio de las observaciones para un factor a un nivel de factor determinado. Minitab grafica la media para cada nivel de factor en la gráfica.
| Media de Factor A al iésimo nivel: |
 |
| Media de Factor B al jésimo nivel: |
 |
Notación
| Término | Description |
|---|---|
| yi. | suma de todas las observaciones para el iésimo nivel de factor A |
| y.j. | suma de todas las observaciones para el jésimo nivel de factor B |
| a | número de niveles en A |
| b | número de niveles en B |
| n | número de casos en el iésimo nivel de factor A y el jésimo nivel de factor B |
Mediana principal (línea central)
Fórmula
El promedio de todas las observaciones en la muestra. Minitab utiliza la mediana principal como la línea central en la gráfica de los efectos principales.

Notación
| Término | Description |
|---|---|
| y... | la suma de todas las observaciones en la muestra |
| a | número de niveles en A |
| b | número de niveles en B |
| n | número de casos en el iésimo nivel del factor A y el jésimo nivel del factor B |
Límites de decisión inferiores y superiores de los efectos principales
Los límites de decisión indican si las medias del nivel de factor son diferentes de la media principal. Los puntos que se ubican fuera del límite de decisión superior (UDL) o del límite de decisión inferior (LDL) son estadísticamente diferentes de la media principal.
El cálculo de los límites de decisión superiores e inferiores varían con base en el número de niveles en el factor y el número de observaciones en cada nivel. Las fórmulas de abajo muestran los límites de decisión superior e inferior para el factor A. Para calcular los límites de decisión para el factor B, sustituya los términos específicos del factor A por términos equivalentes para el factor B.
Factor de dos niveles
Los límites de decisión superiores e inferiores del factor A son:
- UDLA =
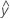 ...+ (.5) * hα* raízcuad[(MSE) * (2 / n1)]
...+ (.5) * hα* raízcuad[(MSE) * (2 / n1)] - LDLA =
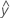 ...- (.5) * hα* α[(MSE) * (2 / n1)]
...- (.5) * hα* α[(MSE) * (2 / n1)]
donde ha = valor absoluto(t(a / 2; abn - ab), MSE = cuadrado medio del error (de un análisis ANOVA con términos A, B y AB) y n1= número de observaciones en cada nivel del factor A.
Factor con más de dos niveles
- UDLA =
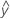 ...+ hα* Sqrt[MSE * (a - 1) / (a * n1)]
...+ hα* Sqrt[MSE * (a - 1) / (a * n1)] - LDLA =
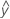 ...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
donde MSE = cuadrado medio del error (de un análisis ANOVA con términos A, B y AB), a = número de niveles de factor en el factor A, y n1= número de observaciones en cada nivel del factor. El valor crítico hα depende de alfa, el número de medias que se grafican y los grados de libertad para el MSE. Puede encontrar valores para hα en la Tabla B.1 del Apéndice B en Nelson1.
Para valores de alfa que estén fuera del rango de 0.001 y 0.1, los límites de decisión son:
- UDLA =
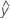 ...+ hα* Sqrt[MSE * (a - 1) / (a * n1)]
...+ hα* Sqrt[MSE * (a - 1) / (a * n1)] - LDLA =
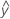 ...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
...- hα* Sqrt[MSE * (a - 1) / (a * n1)]
donde MSE = cuadrado medio del error (de un análisis ANOVA con los términos A, B y AB), n1 = número total de observaciones en cada nivel del factor y hα = valor absoluto (t(α2, gl); donde a2 = (1- (1- a )** (1 / a)) / 2 y gl = nT - ab donde nT = número total de observaciones en la muestra.
- L.S. Nelson (1983). “Exact Critical Values for Use with the Analysis of Means”, Journal of Quality Technology, 15, 40--44.
Límites de decisión inferiores y superiores de los efectos de interacción
Los límites de decisión indican si la interacción es significativa. Los puntos que se ubican fuera del límite de decisión superior (UDL) o del límite de decisión inferior (LDL) indican que la interacción es estadísticamente significativa.
Abajo se indican las fórmulas generales para los límites de decisión superior e inferior para la interacción de los factores A y B. Los términos se definen de manera diferente en función del número de niveles y observaciones en cada factor.
- UDLAB = hα* raízcuad[MSE * (q / (a * b * n)]
- LDLAB = –hα* raízcuad[MSE * (q / (a * b * n)]
donde ha = valor absoluto (t(α2, dfe)), a = número de niveles en el factor A, b = número de niveles en el factor B, n = número de observaciones de cada interacción entre factores, q = grados de libertad para los efectos de interacción, (a - 1)(b - 1) y dfe = grados de libertad para el error, abn - ab.
Factores A y B ambos tienen dos niveles
- α2 = a / 2
El Factor A tiene dos niveles y el Factor B tiene más de dos niveles
- α2 = (1- (1- a )** (1 / b)) / 2
donde a = número de niveles en el factor A y b = número de niveles en el factor B.
El Factor A tiene más de dos niveles y el Factor B tiene dos niveles
- α2 = (1- (1- a )** (1 / a)) / 2
donde a = número de niveles en el factor A y b = número de niveles en el factor B.
Los Factores A y B tienen más de dos niveles
- α2 = (1- (1- a )** (1 /a * b)) / 2
donde a = número de niveles en el factor A y b = número de niveles en el factor B.
