En este tema
Método
El análisis de medias es un procedimiento para determinar si las medias del nivel de factor individual son diferentes de la media principal (la media de todas las observaciones en un factor). A continuación se enumeran los pasos que Minitab utiliza para calcular los resultados ANOM para un modelo de un solo factor:
- Calcula la media en cada nivel del factor, y̅i. (i = 1, …, r).
- Calcula la media principal de todas las observaciones, y….
- Calcula sp, un estimado de la desviación estándar de la observación.
- Determina el valor hα, que es el valor correspondiente al nivel de significancia elegido para la prueba y se utiliza en las líneas de decisión inferiores y superiores.
- Calcula los límites de decisión inferiores (LDL) y superiores (UDL).
- Grafica las medias de cada nivel de factor con líneas de referencia superiores e inferiores, y la línea central en la media principal.
Media
Fórmula
El promedio de las observaciones a cada nivel de factor. Minitab grafica la media para cada nivel de factor en la gráfica.
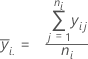
Notación
| Término | Description |
|---|---|
| ni | número de observaciones a nivel del factor i |
| yij | valor de la jésima observación al iésimo nivel del factor |
Mediana principal (línea central)
Fórmula
El promedio de todas las observaciones para todos los niveles del factor. Minitab utiliza la mediana principal como la línea central en la gráfica.
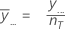
Notación
| Término | Description |
|---|---|
| y... | la suma de todas las observaciones en la muestra |
| nT | número total de observaciones |
Desviación estándar (Desv.Est.)
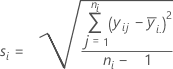
Notación
| Término | Description |
|---|---|
| yij | observaciones al i ésimo nivel del factor |
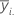 | media de observaciones al i ésimo nivel factor del factor |
| ni | número de observaciones al i ésimo nivel del factor |
Desviación estándar agrupada
Un estimado de la variación para todos los niveles del factor. La desviación estándar agrupada se utiliza para calcular los límites de decisión.
Fórmula
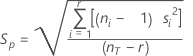
Notación
| Término | Description |
|---|---|
| r | número de niveles |
| nT | número total de observaciones |
Límites de decisión inferiores y superiores
Los límites de decisión indican si las medias del nivel de factor son diferentes de la media principal. Los puntos que se ubican fuera del límite de decisión superior (UDL) o del límite de decisión inferior (LDL) son estadísticamente diferentes de la media principal.
El cálculo de los límites de decisión superiores e inferiores varían con base en el número de niveles en el factor y el número de observaciones en cada nivel.
Factor de dos niveles con un número de observaciones iguales en cada nivel
- UDL = y.. + hα sp* raízcuad(1/ nT)
- LDL = y.. - hα sp* raízcuad(1/ nT)
donde hα = valor absoluto (t(a / 2, nT - 2)), sp = desviación estándar agrupada y nT = número total de observaciones.
Factor con más de 2 niveles con un igual número de observaciones en cada nivel
- UDL = y.. + hα sp* raízcuad[(r-1) / (rn1)]
- LDL = y.. - hα sp* raízcuad[(r-1) / (rn1)]
donde r = número de niveles en el factor y n1 = número de observaciones en cada nivel.
Los grados de libertad son (n1- 1) * r.
Para valores de alfa que estén fuera del rango de 0.001 y 0.1, los límites de decisión son:
- UDL = y.. + hα sp* raízcuad[(nT - n1) / (nT* n1)]
- LDL = y.. - hα sp* raízcuad[(nT - n1) / (nT* n1)]
donde hα = valor absoluto (t(α2, df) y α2 = (1- (1- a )** (1 / r)) / 2 y gl = nT - r.
Para obtener el hα de los valores de α entre 0.001 y 0.1 véase Nelson1.
Factor con 2 o más niveles con un número desigual de observaciones en cada nivel
- UDLi = y.. + hα sp* raízcuad[(nT - ni) / (nT* ni)]
- LDLi = y.. - hα sp* raízcuad[(nT - ni) / (nT* ni)]
- L.S. Nelson (1983). "Exact Critical Values for Use with the Analysis of Means", Journal of Quality Technology, 15, 40-44.
