En este tema
Gráfica Análisis de medias para datos que siguen la distribución normal
Utilice la gráfica de análisis de medias para datos normalmente distribuidos a fin de determinar si los efectos principales y los efectos de interacción en los datos son estádísticamente significativos. Con base en el número de factores en el diseño, la gráfica muestra una gráfica de efectos principales o dos gráficas de efectos principales, y una gráfica de efectos de interacción.
- Gráfica de efectos de interacción
-
Utilice la gráfica de efectos de interacción para probar la hipótesis nula de que no hay una interacción entre los factores. Minitab muestra una gráfica de efectos de interacción solamente cuando los datos incluyen dos factores.
La gráfica de efectos de interacción muestran la medición promedio de cada combinación de niveles de factores. Minitab grafica la línea central en cero, lo cual no representa ningún efecto de interacción. Los límites de decisión se calculan con base en los datos y en el nivel de significancia que se especifique. Con un análisis de medias de dos factores, evalúe primero los efectos de interacción. Si los efectos de interacción son estadísticamente significativos, usted no puede interpretar los efectos principales sin considerar los efectos de interacción.
Utilice los límites de decisión para probar las hipótesis de los efectos de interacción de la manera siguiente:- Si uno o más efectos están fuera de los límites de decisión, se puede concluir que el efecto de interacción entre los dos factores es estadísticamente significativo. Identificar los puntos que están más allá de los límites de decisión puede ayudarle a interpretar la interacción.
- Si no hay efectos fuera de los límites de decisión, entonces no puede rechazar la hipótesis. No hay suficiente evidencia para concluir que hay un efecto de interacción.
- Gráfica de efectos principales
-
Utilice la gráfica de efectos principales para probar la hipótesis nula de que cada media poblacional para cada nivel del factor es igual a la media de la población general en el nivel de significancia que specifique. Minitab muestra una gráfica de efectos principales para cada factor.
La gráfica de efectos principales muestra la medición promedio de cada nivel de factor. La línea central es el promedio general de todas las muestras. Los límites de decisión se calculan con base en los datos y en el nivel de significancia que se especifique. Utilice los límites de decisión para probar las hipótesis de efectos principales como sigue:- Si una media de muestra se ubica fuera de los límites de decisión, se puede rechazar la hipótesis nula y concluir que la diferencia entre la media grupal y la media general es estadísticamente significativa.
- Si una media de muestra se encuentra dentro de los límites de decisión, no se puede rechazar la hipótesis nula. No hay suficiente evidencia para concluir que la media grupal y la media general sean diferentes.
Si los niveles de factor tienen el mismo número de observaciones, los límites de decisión son líneas rectas. Si los niveles no tienen el mismo número de observaciones, los límites de decisión cambian con el nivel.
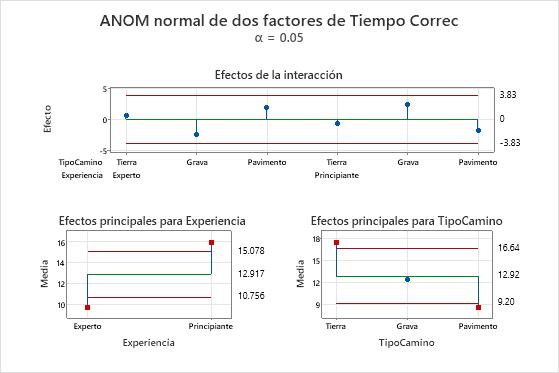
Resultados clave: Gráfica de efectos principales, gráfica de efectos de interacción
En esta gráfica, los efectos de interacción se encuentran claramente dentro de los límites de decisión, lo que indica que los efectos de interacción no son estadísticamente significativos. A continuación, evalúe los efectos principales. Las dos gráficas inferiores muestran las medias de los niveles de los dos factores. El efecto principal es la diferencia entre la media y la línea central.
En la gráfica de efectos principales para la experiencia, los puntos que representan las medias de los niveles de los factores para la experiencia tanto de expertos como de principiantes están fuera de los límites de decisión. Esta condición indica que la diferencia entre cada una de estas medias y la media general es estadísticamente significativa. Usted puede concluir que los conductores expertos tienen un tiempo medio de corrección significativamente inferior y los conductores principiantes tienen un tiempo medio de corrección significativamente superior.
De manera similar, en la gráfica de efectos principales del tipo de carretera, los efectos principales de carreteras de tierra y pavimentadas están fuera de los límites de decisión, lo que indica que estos efectos principales son estadísticamente significativos. Sin embargo, el efecto principal de las carreteras de grava no es estadísticamente significativo.
Gráfica Análisis de medias para datos binomiales
Utilice la gráfica Análisis de medias para datos binomiales para identificar proporciones excepcionalmente grandes o pequeñas.
- Si una proporción de muestra se ubica más allá de un límite de decisión, se puede rechazar la hipótesis nula y concluir que la diferencia entre la proporción del grupo y la población general es estadísticamente significativa.
- Si una proporción de muestra se encuentra dentro de los límites de decisión, no se puede rechazar la hipótesis nula. No hay suficiente evidencia para concluir que la proporción de grupo y la proporción general sean diferentes.
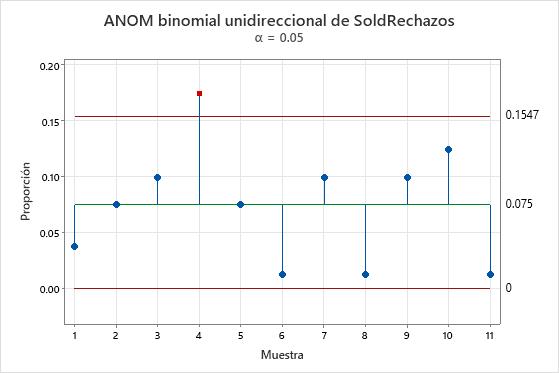
Resultados clave: Gráfica de ANOM binomial de un solo factor
En esta gráfica, la proporción de soldaduras defectuosas en la muestra 4 está por encima de los límites de decisión. La diferencia entre la proporción de soldaduras defectuosas en este grupo y la proporción general es estadísticamente significativa.
Gráfica de análisis de medias para datos de Poisson
Utilice la gráfica de análisis de medias para datos de Poisson para identificar tasas de ocurrencia pequeñas o extrañamente altas.
- Si una tasa de ocurrencia se encuentra por encima o por debajo de un límite de decisión, se puede rechazar la hipótesis nula y concluir que la diferencia entre la tasa de ocurrencia de grupo y la tasa de ocurrencia general es estadísticamente significativa.
- Si una media de muestra se encuentra dentro de los límites de decisión, no se puede rechazar la hipótesis nula. No hay suficiente evidencia para concluir que la tasa de ocurrencia de grupo y la tasa de ocurrencia general son diferentes.
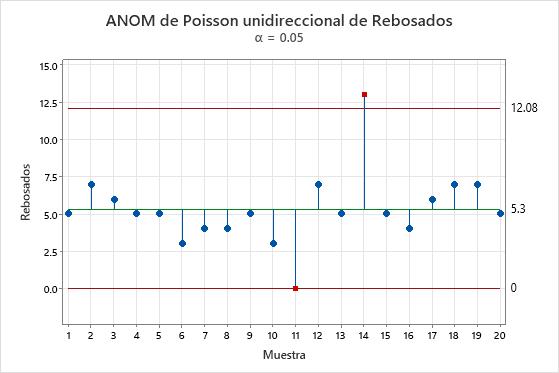
Resultados clave: Gráfica de ANOM Poisson de un solo factor
En esta gráfica, la máquina 11 tiene un conteo de llenado excesivo de 0, que es extrañamente pequeño. La máquina 14 tiene un conteo de llenado excesivo de 13, que es extrañamente grande. El gerente programa un trabajo de diagnóstico para la máquina 14 con el fin de descartar cualquier problema mecánico.
