Todos los informes de capacidad del proceso para Informe de proceso

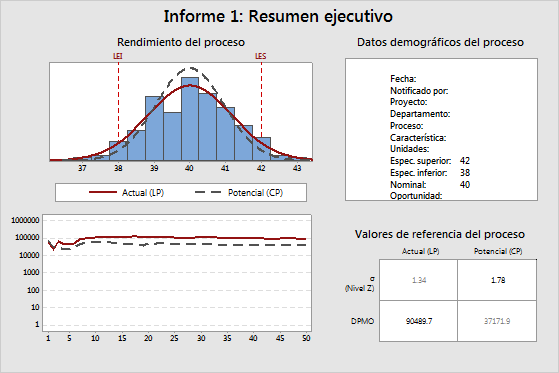
Gráfica de la parte superior de desempeño del proceso: Rendimiento estático del proceso LP/CP

Las curvas normales en el histograma muestran la distribución estimada de las mediciones CTQ del proyecto. CTQ (crítico para la calidad) se refiere a las principales características medibles de un producto o proceso cuyas normas de desempeño se deben cumplir a fin de satisfacer al cliente. Los CTQ pueden incluir cualquier variable relacionada con el producto o servicio y tener los límites de especificación superior e inferior.

Minitab calcula estas curvas a partir de las estimaciones a largo plazo (LP) y a corto plazo (CP) de la media del proceso y de la desviación estándar del proceso. Luego, dibuja una curva normal LP y una curva normal CP. En casi todos los casos, la curva normal LP es más amplia que la curva normal CP.

Los límites de especificación (LEI y LES) proveen puntos de referencia. El valor objetivo (valor nominal) está centrado por lo general, pero no siempre, entre los límites de especificación inferior y superior. De manera ideal, la media debería estar cerca del valor objetivo. En el ejemplo anterior, la media del proceso parece estar muy cerca del valor objetivo.

Gráfica de la parte inferior de desempeño del proceso: Rendimiento dinámico del proceso LP/CP

Esta gráfica muestra el valor acumulado estimado de DPMO (defectos por millón de oportunidades) después de cada subgrupo de datos, tanto para LP (largo plazo) como CP (corto plazo). Minitab calcula DPMO obteniendo primero un Nivel Z después de cada subgrupo, que luego convierte en un DPMO. Los valores de Nivel Z son funciones de la media y la desviación estándar estimadas, tanto para LP como para CP.

Si el proceso es estable, entonces las líneas de esta gráfica se aproximan a un valor constante. Si las líneas no se estabilizan, o el proceso no es estable o no hay suficientes datos. En el ejemplo anterior, ambas líneas tienden a fluctuar en el lado izquierdo de la gráfica, pero luego se estabilizan en el lado derecho de la gráfica. Si las líneas fueran relativamente planas en la izquierda de la gráfica, luego hay un aumento o una disminución constante. Esto indica que algo en el proceso pudiera haberse modificado: la media se desplazó o hubo un cambio en la variación del proceso. En la mayoría de los casos, la línea LP está por encima de la línea CP, porque el valor de Z.Bench LP es más pequeño que el valor de Z.Bench CP, debido a la influencia de cambios rápidos y graduales del proceso.

Las dos líneas de esta gráfica deberían oscilar hacia arriba y hacia bajo en el lado izquierdo, donde hay pocos subgrupos, pero deberían estabilizarse en el lado derecho si se han recolectado suficientes datos y el proceso es estable. Si las líneas no se estabilizan, las gráficas del Informe 4, Estadísticos acumulados, le ayudarán a determinar si el problema se debe a insuficiencia de datos o a una inestabilidad del proceso.

Datos demográficos del proceso

La tabla de datos demográficos muestra información del proyecto y del proceso que usted especifique.

Valores de referencia del proceso

Los números en negrita son Sigma CP (o Nivel Z) y DPMO LP. La mayoría de los Black Belts notifican rendimiento del proceso utilizando estos dos valores.

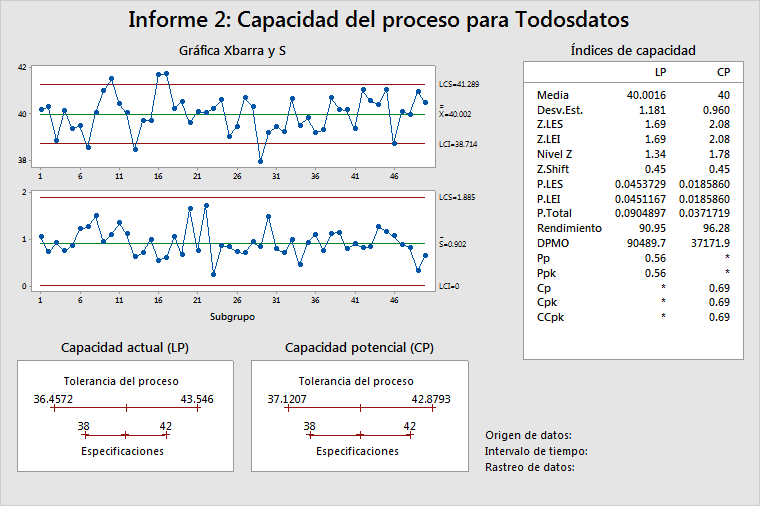
Gráficas de control de los datos del proceso

Muestra la estabilidad del proceso durante el tiempo de la recolección de los datos. Para subgrupos mayores que 1, utilice una gráfica Xbarra para determinar la estabilidad de la media del proceso y una gráfica S para determinar la estabilidad de la desviación estándar del proceso. Si el tamaño del subgrupo = 1, Minitab muestra una gráfica I y una gráfica MR.

Gráficas de capacidad LP/CP

Muestra la tolerancia estimada del proceso en relación con los límites de especificación. La tolerancia del proceso es el punto de centrado del proceso ± 3 desviaciones estándar. Hay dos gráficas porque el punto de centrado del proceso y la desviación estándar del proceso son diferentes para LP y CP. LP utiliza la media del proceso como punto de centrado, mientras que CP utiliza el objetivo (o punto intermedio entre especificaciones o la media del proceso cuando solo se indica una especificación) como punto de centrado. Vea Cómo Minitab elige centrar valores para estadísticos a corto plazo para Informe de proceso para obtener más información.

En otras palabras, estas gráficas muestran si un vehículo (el proceso) cabrá en un garaje (las especificaciones) o incluso si el vehículo está centrado en el garaje. En el ejemplo anterior, el proceso es más ancho que las especificaciones. Sin embargo, el proceso está centrado, como se ilustra en la gráfica LP, que muestra que el punto de centrado del proceso (media) casi igual que el objetivo.

Índices de capacidad LP/CP

Muestra los estadísticos comúnmente utilizados para notificar el desempeño del proceso. Vea Explicación de las medidas de capacidad para una comparación de los estadísticos que miden el desempeño a largo plazo (LP) y a corto plazo (CP).

Utilice los valores de Nivel Z para describir el desempeño del proceso. Los estadísticos de Nivel Z no solo se basan en las condiciones apropiadas del proceso, sino que también conducen directamente a estimaciones de la probabilidad de un defecto: PPM, DPMO, y así sucesivamente. Las alternativas aceptables son CCpk y Ppk, porque se basan en las mismas condiciones del proceso que los estadísticos de Nivel Z.

Para obtener más información sobre cálculos específicos, vaya a Cálculos de los estadísticos y valores de capacidad del proceso para Informe de proceso.

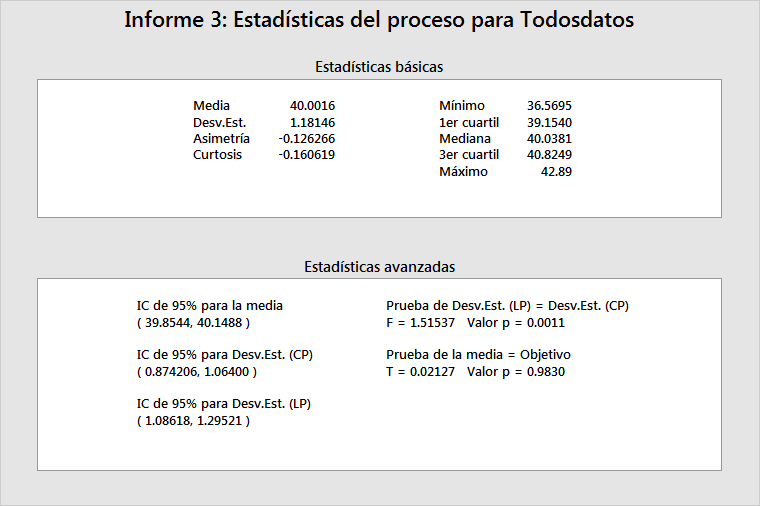
Estadísticas básicas

Esta tabla provee la media del proceso (media LP), la desviación estándar del proceso (desviación estándar LP), así como otras estadísticas básicas.

Utilice la asimetría y la curtosis para ayudar a determinar si los datos están distribuidos normalmente. Sin embargo, las gráficas de probabilidad son mucho más útiles. (En el Informe 6, la gráfica normal estima la probabilidad de un defecto.)

El mínimo, 1^er cuartil, mediana, 3^es cuartil y máximo muestran la dispersión de los datos. Por ejemplo, 25% de los datos no son mayores que 39.1540 (1^er cuartil), 50% de los datos no son mayores que 40.0381 (mediana) y 75% de los datos no son mayores que 40.8249 (3^er cuartil).

Estadísticos avanzados

Esta tabla provee inferencias estadísticas para los parámetros del proceso, la media CP y la desviación estándar.

La media del proceso incluye un intervalo de confianza de 95% y estadísticos de prueba para mostrar si la media del proceso es igual al objetivo del proceso. Si la media del proceso y el objetivo del proceso no tienen diferencia estadísticamente significativa, entonces el valor p será > 0.05 y el objetivo del proceso se encontrará dentro de los bordes del intervalo de confianza. En el ejemplo anterior, la prueba tiene un valor p de 0.9830 y el objetivo (40) se encuentra dentro de los bordes del intervalo de confianza de 95% para la media. Usted no puede rechazar la hipótesis nula de que la media del proceso es igual al objetivo del proceso.

La tabla también provee intervalos de confianza de 95% para desviaciones estándar tanto LP como CP, así como una prueba para determinar si estas dos cantidades son iguales. Si no existe una diferencia estadísticamente significativa entre las desviaciones estándar LP y CP del proceso, usted puede concluir que el proceso no exhibe cambios rápidos y/o graduales significativos y que no había causas especiales presentes al momento de recolectar los datos. En el ejemplo anterior, la prueba para varianzas iguales tiene un valor p de 0.0011. Por lo tanto, usted debe rechazar la hipótesis nula y concluir que la desviación estándar tanto LP como CP son significativamente diferentes.

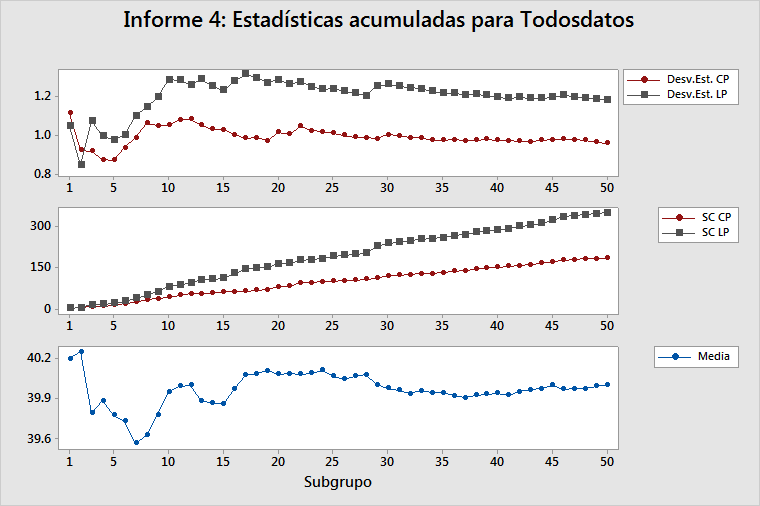
Desv.Est. LP/CP acumulada

Esta gráfica muestra las estimaciones tanto de la desviación estándar LP como de la desviación estándar CP después de cada subgrupo de datos. Debido a que todas las medidas de desempeño del proceso se basan en estimados de la desviación estándar del proceso, usted debe determinar si estas estimaciones son apropiadas. Esto depende de que se tenga un proceso estable (un proceso en el cual la variabilidad inherente no cambia) y suficientes datos para caracterizar el proceso adecuadamente.

Las estimaciones de la desviación estándar LP y la desviación estándar CP deberían oscilar considerablemente en el lado izquierdo de la gráfica, que contiene pocos subgrupos. Si el proceso es estable y usted recolectó suficientes datos, entonces las estimaciones se estabilizarán en el lado derecho de la gráfica. Si las líneas en la gráfica continúan oscilando, entonces o no recolectó suficientes datos o la variación del proceso es inestable.

Para que el proceso sea estable, la separación entre la desviación estándar LP y la desviación estándar CP debe volverse bastante constante. Si el proceso cambia, debido a por ejemplo un desplazamiento en la media o un cambio en la variación, entonces la separación entre la desviación estándar LP y la desviación estándar CP cambia.

Para obtener más información, vaya a Identificar desplazamientos en la media del proceso con el Informe de proceso y Identificar un aumento en la variabilidad del proceso con Informe de proceso.

SC LP/CP acumulada

Esta gráfica muestra tanto la suma de desviaciones cuadráticas (SC Total o SC LP) después de cada subgrupo de datos como la suma de todas las desviaciones cuadráticas dentro de cada subgrupo (SC de corto plazo o SC CP) después de cada subgrupo de datos. Para obtener más información, vaya a Cálculos de sumas de cuadrados para Informe de proceso.

SC CP es una muy buena herramienta de diagnóstico para detectar cambios en la variación inherente de un proceso. Si la variación inherente es estable, entonces la SC de corto plazo de cada subgrupo sería aproximadamente la misma. Por lo tanto, la SC CP debe aumentar en aproximadamente la misma cantidad para cada subgrupo, lo que resulta en una línea de SC CP que tiene una pendiente ascendente constante. Cualquier cambio en la variabilidad inherente del proceso se muestra como un cambio en la pendiente de la línea de SC CP.

SC Total es la suma de SC de corto plazo y SC de subgrupos. Por lo tanto la SC Total es influenciada por la estabilidad de la varianza del proceso y de la media del proceso. Si ambas son estables, entonces la contribución a SC Total será aproximadamente la misma para cada subgrupo. Por lo tanto, la SC LP debe aumentar en aproximadamente la misma cantidad para cada subgrupo, lo que resulta en una línea de SC LP que tiene una pendiente ascendente constante. Cualquier cambio en la variabilidad inherente del proceso se muestra como un cambio en la pendiente de la línea de SC LP.

Un cambio repentino en la variabilidad inherente del proceso afecta SC de corto plazo y SC de subgrupos y cambia las pendientes de las líneas de SC CP y SC LP. Por lo tanto, un cambio en la pendiente de ambas líneas indica un cambio en la variabilidad inherente del proceso.

Un desplazamiento en la media del proceso afecta SC de subgrupos, pero no SC de corto plazo y cambia la pendiente de la línea de SC LP, pero no aquella de la línea de SC CP. Por lo tanto, un cambio en la pendiente de la línea de SC LP, sin ningún cambio en la pendiente de la línea de SC CP, indica un desplazamiento en la media del proceso.

Para obtener más información, vaya a Identificar desplazamientos en la media del proceso con el Informe de proceso y Identificar un aumento en la variabilidad del proceso con Informe de proceso.

Media acumulada

Esta gráfica muestra la estimación de la media del proceso después de cada subgrupo. La adecuación de la estimación de la media del proceso depende de la cantidad de datos que recolectó y la estabilidad del proceso.

Las estimaciones deberían oscilar considerablemente hacia arriba y hacia abajo en el lado izquierdo de la gráfica, que contiene pocos subgrupos. Si el proceso es estable y usted recolectó suficientes datos, entonces las estimaciones se estabilizarán en el lado derecho de la gráfica. Si las líneas continúan oscilando, entonces o no recolectó suficientes datos o la media del proceso cambia dramáticamente. Observe la gráfica de Desv.Est. acumulada para determinar si el problema es que no tiene suficientes datos. Si no tiene suficientes datos, entonces las líneas LP y CP también oscilarán.

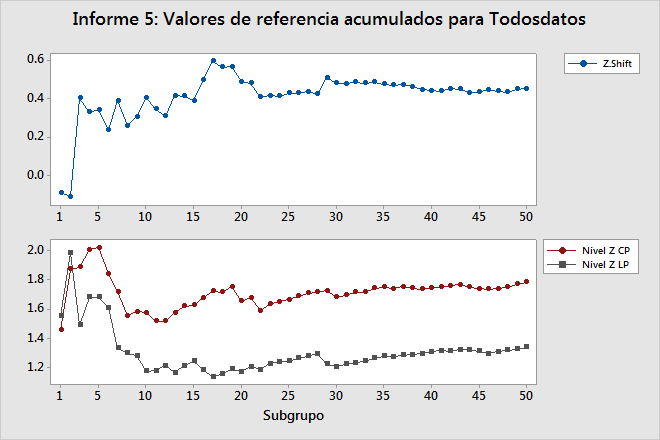
Desplazamiento Z

El desplazamiento Z es igual a la separación entre Nivel Z LP y Nivel Z CP.

La línea de esta gráfica debería oscilar hacia arriba y hacia bajo en el lado izquierdo, que contiene pocos subgrupos, pero debería estabilizarse en el lado derecho si usted ha recolectado suficientes datos y el proceso es estable.

Nivel Z LP y Nivel Z CP

La gráfica de Nivel Z indica si usted recolectó suficientes datos para utilizar estos estadísticos con confianza para notificar el desempeño del proceso. Las dos líneas de esta gráfica deberían oscilar hacia arriba y hacia bajo en el lado izquierdo, que contiene pocos subgrupos, pero deberían estabilizarse en el lado derecho si usted recolectó suficientes datos y el proceso es estable. Si las líneas no se estabilizan, entonces las gráficas del informe Estadísticos acumulados le ayudarán a determinar si el problema es que no tiene suficientes o inestabilidad del proceso.

Tanto la separación en la gráfica de Nivel Z como la línea en la gráfica de desplazamiento Z deben aproximarse a un valor constante, como ocurre en el ejemplo anterior.

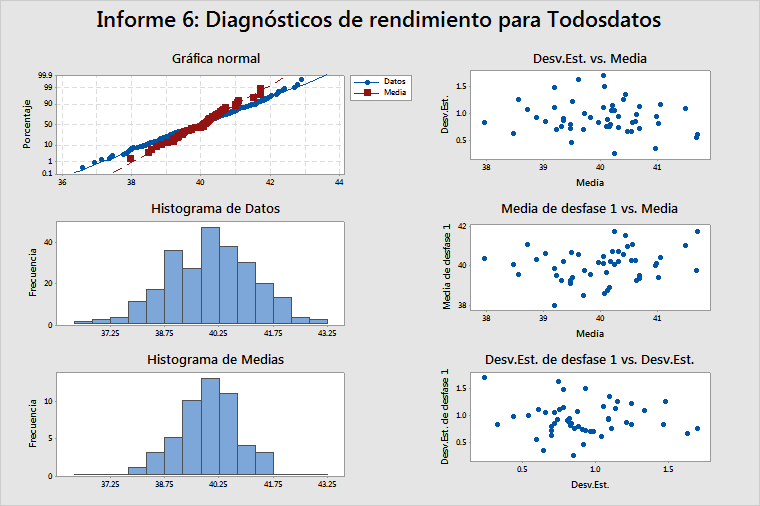
Gráfica normal, histograma de datos e histograma de medias

Estas gráficas ayudan a determinar si los datos son normales. Si los datos son no normales, entonces las estimaciones de probabilidad de un defecto (como por ejemplo DPMO) no serán exactas . En la mayoría de los casos, estas estimaciones tienden a ser menores que los valores reales. Entonces, revise la gráfica normal y los dos histogramas para determinar si los datos son por lo menos razonablemente normales antes de utilizar estimaciones tales como DPMO. Los datos del ejemplo anterior parecen estar distribuidos normalmente.

Si los datos parecen ser demasiado asimétricos, intente corregir el problema utilizando una transformación, como por ejemplo la transformación de Box-Cox. Cuando usted elige Usar transformación de potencia Box-Cox (W=Y^λ) con en el cuadro de diálogo secundario Informe de proceso Opciones, Minitab transforma automáticamente los datos, el objetivo y los límites de especificación. Sin embargo, si transforma manualmente los datos, también debe transformar manualmente el objetivo y los límites de especificación.

Desv.Est. vs. media

Cuando no existe correlación entre las medias de los subgrupos y las desviaciones estándar de los subgrupos, esta gráfica debe mostrar puntos dispersos de forma aleatoria, como en el ejemplo anterior.

Si existe una correlación positiva entre las medias y las desviaciones estándar, entonces las desviaciones estándar de los subgrupos tienden a aumentar a medida que aumentan las medias de los subgrupos. La transformación de Box-Cox (λ = 0) es una transformación ampliamente conocida para estabilizar la varianza que generalmente funciona bien en estos casos.

Media de desfase 1 vs. media

La gráfica de Media de desfase 1 vs. Media es una gráfica de (la media del subgrupo)_i versus (la media del subgrupo)_i–1. Esta gráfica debe mostrar puntos dispersos de forma aleatoria, como en el ejemplo anterior, lo cual indica que no hay correlación entre las medias de subgrupos sucesivos.

Si existe una correlación positiva y una media de subgrupo es mayor que la media general del proceso, también es probable que la siguiente media de subgrupo sea mayor que la media general del proceso. Por lo tanto, una correlación positiva implica que el proceso está sujeto a cambios graduales en la media. Si la correlación es negativa, esto indicaría medias de subgrupos que se alternan —baja, luego alta, luego baja—, no dos medias de subgrupos consecutivas bajas. Esta correlación negativa implica un control excesivo del proceso.

Desv.Est. de desfase 1 vs. Desv.Est.

La gráfica de Desv.Est. de desfase 1 vs. Desv.Est. es una gráfica de (la desviación estándar del subgrupo)_i vs. (la desviación estándar del subgrupo)_i–1. Esta gráfica debe mostrar puntos dispersos de forma aleatoria, como en el ejemplo anterior, para mostrar que no existe correlación entre las desviaciones estándar de subgrupos sucesivos.

Como sucede con las medias de los subgrupos, si existe una correlación positiva y la desviación estándar de un subgrupo es mayor que la desviación estándar promedio de todos los subgrupos, también es muy probable que la desviación estándar del siguiente subgrupo sea mayor que la desviación estándar promedio de todos los subgrupos. Por lo tanto, las desviaciones estándar de los subgrupos tenderían a cambiar gradualmente hacia arriba y hacia bajo. Esta situación puede estar acompañado por medias que también cambian gradualmente hacia arriba y hacia bajo, así como correlación entre las medias de los subgrupos y las desviaciones estándar de los subgrupos. En este caso, pruebe utilizando una transformación de Box-Cox con λ = 0.

Una autocorrelación positiva en las desviaciones estándar de los subgrupos podría ser causada por desgaste de la herramienta u otro deterioro dentro del proceso (lo que ocasiona una variación cada vez mayor) o la presencia de un factor perturbador fuera de control (como por ejemplo la humedad relativa) que tiene influencia en la variación.