En este tema
Métodos para intervalos de tolerancia
Minitab calcula los intervalos de tolerancia tanto paramétricos como no paramétricos. Los cálculos para los intervalos de tolerancia paramétricos presuponen que la distribución original de la muestra está distribuida normalmente. Los cálculos para los intervalos de tolerancia no paramétricos solo presuponen que la distribución original es continua.
Definiciones generales
Sean X1, X2, ..., Xn los estadísticos ordenados con base en una muestra aleatoria de tamaño n proveniente de una distribución continua.
Sea F(χ;θ) la función de distribución para Ω en algún espacio de parámetro con una dimensión mayor que o igual a 1.
Sean L < U dos estadísticos basados en la muestra tal que para cualquier valor α y P dado, con 0 < α < 1 y 0 < P < 1, se cumpla lo siguiente para cada θ en Ω:
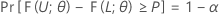
Entonces, el intervalo [L, U] es un intervalo de tolerancia bilateral con contenido = P x 100% y nivel de confianza = 100(1 – α)%. Tal intervalo se puede denominar un intervalo de tolerancia (1 – α, P) bilateral. Por ejemplo, si α = 0.10 y P = 0.85, entonces el intervalo resultante se denomina un intervalo de tolerancia (90%, 0.85) bilateral.
Si L = –∞ y U < +∞, entonces el intervalo (-∞, U] se denomina un borde de tolerancia superior (1 – α, P) unilateral. Si L > -∞ y U = +∞, entonces el intervalo [L, +∞) se denomina un borde de tolerancia inferior (1 – α, P) unilateral.
- Un borde de tolerancia inferior (1 – α, P) unilateral también es un borde de tolerancia superior (α, 1 – P) unilateral.
- Un borde de confianza inferior (1 – α )100% unilateral del percentil (1 – P) de la distribución de los datos es también un borde de tolerancia inferior (1 – α, P) unilateral. Igualmente, un borde de confianza superior (1 – α )100% unilateral del percentil P de la distribución de los datos es también un borde de tolerancia superior (1 – α , P) unilateral.
- Si L y U son los bordes de tolerancia inferior y superior (1 – α/2 , (1 + P )/2) unilaterales, entonces [ L, U ] es un intervalo de tolerancia (1 – α, P ) bilateral aproximado. Este método se puede utilizar en aquellos casos en los que no se pueda obtener intervalos de tolerancia bilaterales. Los intervalos de tolerancia bilaterales resultantes son generalmente conservadores. Véase Guenther1 y Hahn y Meeker2.
- Guenther, W. C. (1972). Tolerance intervals for univariate distributions. Naval Research Logistics, 19: 309–333.
- Hahn G. J. y Meeker W. Q. (1991). Statistical Intervals: A Guide for Practitioners John Wiley & Sons, New York.
Intervalos de tolerancia exactos para distribuciones normales

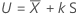
Factor de tolerancia para los intervalos unilaterales
El factor de tolerancia exacto para un intervalo unilateral viene dado por la siguiente ecuación: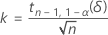
donde tn-1,1-α(δ) es el percentil 1 – α de la distribución t no central con n – 1 grados de libertad y parámetro de no centralidad, δ, que viene dado por la siguiente fórmula:

Factor de tolerancia para los intervalos bilaterales
El factor de tolerancia exacto para un intervalo bilateral se obtiene resolviendo la siguiente ecuación para k. Consulte Krishnamoorthy y Mathew1.
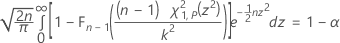
donde Fn – 1 es la función de distribución acumulada para una distribución de chi-cuadrada con n – 1 grados de libertad y χ21,p es el percentil Pésimo de la distribución de chi-cuadrada no central con 1 grado de libertad y parámetro de no centralidad z2. El lado izquierdo de la ecuación puede reescribirse como:
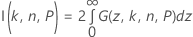
donde:
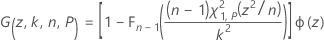
donde Φ(z) es la función de densidad de probabilidad de la distribución normal estándar. Minitab utiliza una cuadratura de Gauss-Legendre de 36 puntos para evaluar I(k, n, P).
Notación
| Término | Description |
|---|---|
| 1 - α | el nivel de confianza del intervalo de tolerancia |
| P | la cobertura del intervalo de tolerancia (el porcentaje mínimo objetivo de la población en el intervalo) |
| G | el límite inferior del intervalo de tolerancia |
| U | el límite superior del intervalo de tolerancia |
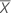 | la media de la muestra |
| k | el factor de tolerancia (también denominado factor k) |
| S | la desviación estándar de la muestra |
| n | el número de observaciones en la muestra |
| ZP | el percentil Pésimo de la distribución normal estándar |
- Krishnamoorthy, K. y Mathew, T. (2009). Statistical Tolerance Regions: Theory, Applications, and Computation. Wiley, Hoboken, NJ.
Intervalos de tolerancia no paramétricos exactos para distribuciones continuas
Minitab calcula intervalos de tolerancia no paramétricos (1 – α, P) exactos, donde 1 – α es el nivel de confianza y P es la cobertura (el porcentaje mínimo objetivo de la población en el intervalo). El método no paramétrico para intervalos de tolerancia es un método independiente de la distribución. Es decir, el intervalo de tolerancia no paramétrico no depende de la población original de la muestra. Minitab utiliza un método exacto para intervalos tanto unilaterales como bilaterales.
Sean X 1, X 2 , ... , X n los estadísticos ordenados con base en una muestra aleatoria de cierta población F(x;θ) distribuida continuamente. Entonces, según lo determinado por Wilks1, 2 y Robbins3, se puede mostrar que:

donde B denota la función de distribución acumulada de la distribución beta con los parámetros a = r y b = n – s + 1. Por lo tanto, ( Xr , Xs ) es un intervalo de tolerancia independiente de la distribución, porque la cobertura del intervalo tiene una distribución beta con valores de parámetros conocidos, que son independientes de la distribución de la población original, F(x;θ).
Intervalos unilaterales
Sea k el entero más grande que satisface lo siguiente:

donde Y es una variable aleatoria binomial con los parámetros n y 1 – P. Se puede indicar (véase Krishnamoorthy y Mathew4) que un borde de tolerancia inferior (1 – α, P) unilateral viene dado por Xk. Del mismo modo, un borde de tolerancia superior (1 – α, P) unilateral viene dado por Xn - k +1. En ambos casos, la cobertura real o efectiva viene dada por P(Y > k).
Intervalos bilaterales
Sea k el entero más pequeño que satisface lo siguiente:

donde V es una variable aleatoria binomial con los parámetros n y P. Por lo tanto,
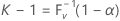
donde F V -1(x) es la función de distribución acumulada inversa de V. Se puede indicar (véase Krishnamoorthy y Mathew4) que un intervalo de tolerancia (1 – α, P) bilateral pudiera obtenerse como ( Xr , Xs ). Minitab elige s = n - r + 1 tal que r = ( n – k + 1) / 2. Tanto r como s se redondean por defecto al entero más cercano. La cobertura real o efectiva viene dada por P(V < k – 1).
Notación
| Término | Description |
|---|---|
| 1 – α | el nivel de confianza del intervalo de tolerancia |
| P | la cobertura del intervalo de tolerancia (el porcentaje mínimo objetivo de la población en el intervalo) |
| n | el número de observaciones en la muestra |
- Wilks, S. S. (1941). Sample size for tolerance limits on a normal distribution. The Annals of Mathematical Statistics, 12, 91–96.
- Wilks, S. S. (1941). Statistical prediction with special reference to the problem of tolerance limits. The Annals of Mathematical Statistics, 13, 400–409.
- Robbins, H. (1944). On distribution-free tolerance limits in random sampling. The Annals of Mathematical Statistics, 15, 214–216.
- Krishnamoorthy, K. y Mathew, T. (2009). Statistical Tolerance Regions: Theory, Applications, and Computation. Wiley, Hoboken, NJ.
