En este tema
Paso 1: Evaluar la normalidad de los datos
Minitab proporciona intervalos de tolerancia para el método normal y el método no paramétrico. Si usted puede presuponer con seguridad que sus datos siguen una distribución normal, entonces puede utilizar el intervalo de tolerancia del método normal. Si no puede presuponer con seguridad que sus datos siguen una distribución normal, entonces debe usar el intervalo de tolerancia del método no paramétrico.
Para determinar si usted puede presuponer que los datos siguen una distribución normal, compare el valor p de la prueba de normalidad con el nivel de significancia (α). Un nivel de significancia de 0,05 indica un riesgo de 5% de concluir que los datos no siguen una distribución normal, cuando los datos sí siguen una distribución normal.
- Valor p ≤ α: Los datos no siguen una distribución normal (Rechazar H0)
- Si el valor p es menor que o igual al nivel de significancia, puede concluir que sus datos no siguen una distribución normal. En este caso, debe utilizar el intervalo de tolerancia del método no paramétrico.
- Valor p > α: Usted no tiene suficiente evidencia para concluir que los datos no siguen una distribución normal (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, usted no tiene suficiente evidencia para concluir que los datos no siguen una distribución normal. En este caso, puede utilizar el intervalo de tolerancia del método normal.
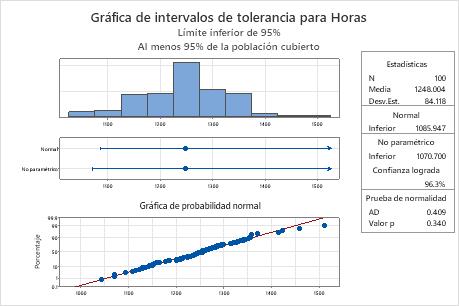
Resultados clave: Valor p
En estos resultados, el valor p es 0,340, que es mayor que el nivel de significancia de 0,05. Debido a que usted puede presuponer que sus datos siguen una distribución normal, puede utilizar el intervalo de tolerancia del método normal.
Paso 2: Examinar el intervalo de tolerancia del método adecuado
- Bilateral
- Utilice un intervalo bilateral para determinar el intervalo que contenga un cierto porcentaje de las mediciones de la población.
- Límite superior
- Utilice un borde superior para determinar el intervalo que indique que un cierto porcentaje de las mediciones de la población no será mayor que un límite superior.
- Límite inferior
- Utilice un borde inferior para determinar el intervalo que indique que un cierto porcentaje de las mediciones de la población no será menor que un límite inferior.
