En este tema
Nivel de confianza
Puesto que las muestras de datos son aleatorias, es poco probable que dos muestras de la misma población produzcan intervalos de tolerancia idénticos. Sin embargo, si usted recolecta muchas muestras, cierto porcentaje de los intervalos de tolerancia resultantes contendrá la proporción mínima de la población que usted especifique.
El nivel de confianza es la probabilidad de que el intervalo de tolerancia realmente incluya el porcentaje mínimo. Por ejemplo, un ingeniero desea saber el rango dentro del cual se encontrará el 99% del producto futuro, con una confianza de 98%. 98% es el nivel de confianza para el intervalo de confianza.
Método
| Nivel de confianza | 98% |
|---|---|
| Porcentaje de población en el intervalo | 99% |
Nota
Usted puede especificar el nivel de confianza del análisis en el cuadro de diálogo Opciones. Minitab muestra el nivel de confianza objetivo en la tabla Métodos. Por opción predeterminada, el nivel de confianza es 95%. Para el método no paramétrico, Minitab calcula el nivel de confianza alcanzado. El nivel de confianza alcanzado es el nivel de confianza exacto que calcula Minitab. El nivel de confianza alcanzado es generalmente mayor que o igual al nivel de confianza objetivo, a menos que el tamaño de su muestra sea demasiado pequeño.
Porcentaje de la población en el intervalo
El porcentaje de la población en el intervalo es el porcentaje mínimo de la población que usted desea que esté incluido en el intervalo de tolerancia. Por ejemplo, un ingeniero desea saber el rango que incluirá el 99% del producto futuro, con una confianza de 98%. 99% es el porcentaje de la población en el intervalo de tolerancia.
Método
| Nivel de confianza | 98% |
|---|---|
| Porcentaje de población en el intervalo | 99% |
N
El tamaño de la muestra (N) es el número total de observaciones en la muestra. En estos datos, el tamaño de la muestra es 400.
Estadísticas
| Variable | N | Media | Desv.Est. |
|---|---|---|---|
| C1 | 400 | 0.604 | 3.671 |
Media
La media resume los valores de la muestra con un valor individual que representa el centro de los datos. La media es el promedio de los datos, que es la suma de todas las observaciones dividida entre el número de observaciones.
En estos datos, la media es 0.604.
Estadísticas
| Variable | N | Media | Desv.Est. |
|---|---|---|---|
| C1 | 400 | 0.604 | 3.671 |
Desv.Est.
La desviación estándar es la medida de dispersión más común, que indica qué tan dispersos están los datos con respecto a la media.
Una mayor desviación estándar indica que los datos están dispersos más ampliamente alrededor de la media y producirán un intervalo de tolerancia más ancho. Una menor desviación estándar indica que los datos están distribuidos más cerca alrededor de la media y producirán un intervalo de tolerancia más estrecho.
En estos resultados, la desviación estándar es 3.671.
Estadísticas
| Variable | N | Media | Desv.Est. |
|---|---|---|---|
| C1 | 400 | 0.604 | 3.671 |
Método normal
Los intervalos de tolerancia son un rango de valores para una característica de calidad específica de un producto que probablemente abarque un porcentaje especificado de los productos fabricados en el futuro. Utilice el el intervalo de tolerancia del método normal si usted puede suponer sin riesgo que su muestra proviene de una población distribuida normalmente.
Si los datos siguen una distribución normal, entonces el método normal es más preciso y económico que el método no paramétrico. El método normal permite alcanzar márgenes de error más pequeños con menos observaciones.
El método normal no es robusto ante las desviaciones severas de la normalidad. Si tiene dudas sobre la distribución original o sabe que la distribución original no es normal, entonces utilice el método no paramétrico.
Interpretación
- Bilateral
- Utilice un intervalo bilateral para determinar el intervalo que contenga un cierto porcentaje de las mediciones de la población.
- Borde superior
- Utilice un borde superior para determinar el intervalo que indique que un cierto porcentaje de las mediciones de la población no será mayor que un límite superior.
- Borde inferior
- Utilice un borde inferior para determinar el intervalo que indique que un cierto porcentaje de las mediciones de la población no será menor que un límite inferior.
Método no paramétrico
Los intervalos de tolerancia son un rango de valores para una característica de calidad específica de un producto que probablemente abarque una proporción especificada de los productos fabricados en el futuro. Si usted no puede presuponer de manera segura que la muestra proviene de una población distribuida normalmente, debe utilizar el intervalo de tolerancia del método no paramétrico.
El método no paramétrico solo requiere que los datos sean continuos. Sin embargo, el método no paramétrico requiere tamaños de muestra más grandes para que los resultados sean exactos. Si el tamaño de la muestra no es lo suficientemente grande, el intervalo no paramétrico es un intervalo no informativo que va desde el infinito negativo al infinito. En ese caso, Minitab muestra un intervalo finito de acuerdo con el rango de los datos. Como resultado, el nivel de confianza alcanzado es mucho menor que el nivel de confianza objetivo.
Interpretación
- Bilateral
- Utilice un intervalo bilateral para determinar el intervalo que contenga un cierto porcentaje de las mediciones de la población.
- Borde superior
- Utilice un borde superior para determinar el intervalo que indique que un cierto porcentaje de las mediciones de la población no será mayor que un límite superior.
- Borde inferior
- Utilice un borde inferior para determinar el intervalo que indique que un cierto porcentaje de las mediciones de la población no será menor que un límite inferior.
Confianza alcanzada
Para el método no paramétrico, Minitab calcula el nivel de confianza alcanzado. Este es el nivel de confianza exacto obtenido a partir de la muestra. Por lo general, será mayor que o igual al nivel de confianza objetivo, a menos que el tamaño de la muestra sea demasiado pequeño.
Interpretación
- Bilateral
- Utilice un intervalo bilateral para determinar el intervalo que contenga un cierto porcentaje de las mediciones de la población.
- Borde superior
- Utilice un borde superior para determinar el intervalo que indique que un cierto porcentaje de las mediciones de la población no será mayor que un límite superior.
- Borde inferior
- Utilice un borde inferior para determinar el intervalo que indique que un cierto porcentaje de las mediciones de la población no será menor que un límite inferior.
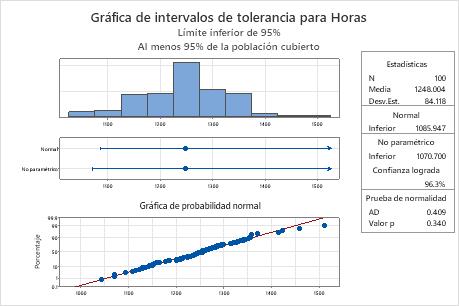
Gráfica de intervalos de tolerancia
- Histograma: Muestra la distribución de los datos de la muestra. Cada barra del histograma representa la frecuencia de los datos dentro de un intervalo.
- Gráficas de intervalos: Muestran la media y los bordes superior y/o inferior del intervalo de tolerancia de cada método. Una línea vertical al final del intervalo representa un borde y una flecha indica que no hay borde para ese lado del intervalo.
- Gráfica de probabilidad normal: Muestra qué tan bien se ajustan sus datos a la distribución normal. Si sus datos están distribuidos normalmente, entonces los puntos de datos en la gráfica de probabilidad formarán una línea recta.
- Tabla Estadísticos: Muestra el tamaño de la muestra, media y desviación estándar.
- Tabla normal: Muestra los bordes superior y/o inferior del intervalo de tolerancia del método normal.
- Tabla No paramétrica: Muestra los bordes superior y/o inferior del intervalo de tolerancia del método no paramétrico y el nivel de confianza alcanzado.
- Tabla de prueba de normalidad: Muestra el valor p y el valor de la prueba de normalidad de Anderson-Darling. Para determinar si usted puede presuponer que los datos siguen una distribución normal, compare el valor p de la prueba de normalidad con el nivel de significancia (α). Si el valor p es menor que o igual al nivel de significancia, puede concluir que sus datos no siguen una distribución normal. En este caso, debe utilizar el intervalo de tolerancia del método no paramétrico.
Interpretación
La gráfica de probabilidad normal muestra que los puntos graficados forman una línea recta aproximada, lo que indica que los datos siguen una distribución normal. Además, el valor p de la prueba de normalidad es 0,340, que es mayor que el nivel de significancia (α = 0,05). Por lo tanto, no existe suficiente evidencia para concluir que los datos no siguen una distribución normal. El ingeniero puede utilizar los resultados del método normal.
El borde inferior normal es 1085,947, por lo que el ingeniero está 95% seguro de que por lo menos 95% de todas las bombillas supera aproximadamente el tiempo de duración de 1086 horas. Para todas las bombillas, el tiempo medio de duración es aproximadamente 1248 horas y la desviación estándar es aproximadamente 84,1.