Un ingeniero especializado en calidad desea evaluar la vida útil de las bombillas que produce una compañía. El ingeniero recoge una muestra aleatoria de 100 bombillas y registra los tiempos de duración hasta que el producto falla. El ingeniero desea calcular el límite de tolerancia inferior (que es el tiempo de duración excedido por al menos el 95% de todas las bombillas).
- Abra los datos de muestra, DuraciónBombillas.MWX.
- Elija .
- En la lista desplegable, seleccione Una o más muestras, cada una en una columna y luego ingrese Horas.
- Haga clic en Opciones.
- En Intervalo de tolerancia, seleccione Límite inferior.
- Haga clic en Aceptar en cada cuadro de diálogo.
Interpretar los resultados
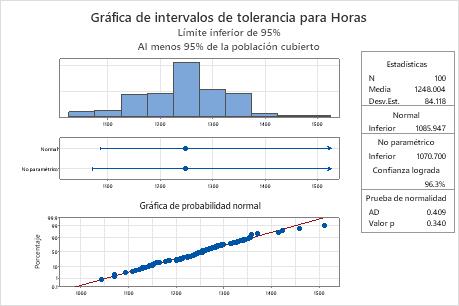
La gráfica de probabilidad normal muestra que los puntos graficados forman una línea recta aproximada, lo que indica que los datos siguen una distribución normal. Además, el valor p de la prueba de normalidad es 0,340, que es mayor que el nivel de significancia (α = 0,05). Por lo tanto, no existe suficiente evidencia para concluir que los datos no siguen una distribución normal. El ingeniero puede utilizar los resultados del método normal.
El borde inferior normal es 1085,947, por lo que el ingeniero está 95% seguro de que por lo menos 95% de todas las bombillas supera aproximadamente el tiempo de duración de 1086 horas. Para todas las bombillas, el tiempo medio de duración es aproximadamente 1248 horas y la desviación estándar es aproximadamente 84,1.
Método
| Nivel de confianza | 95% |
|---|---|
| Porcentaje de población en el intervalo | 95% |
Estadísticas
| Variable | N | Media | Desv.Est. |
|---|---|---|---|
| Horas | 100 | 1248.004 | 84.118 |
Límite de tolerancia normal de 95%
| Variable | Método normal | Método no paramétrico | Confianza lograda |
|---|---|---|---|
| Horas | 1085.947 | 1070.700 | 96.3% |