Estimaciones de máxima verosimilitud
Las estimaciones de máxima verosimilitud de los parámetros en la distribución se calculan maximizando la función de verosimilitud con respecto a los parámetros. Para un conjunto de datos dado, las estimaciones de máxima verosimilitud son los valores más probables para los parámetros de distribución.
El algoritmo de Newton-Raphson se utiliza para calcular las estimaciones de máxima verosimilitud de los parámetros de distribución. El algoritmo de Newton-Raphson es un método numérico iterativo para calcular el máximo de una función. 1
Nota
Minitab calcula las estimaciones de parámetros utilizando el método de máxima verosimilitud para todas las distribuciones, excepto la distribución lognormal. Para la distribución lognormal, Minitab calcula estimaciones de parámetros sin sesgo.
Distribuciones de probabilidades
Distribución lognormal
 |
|
| CDF |
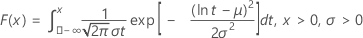 |
| Media |
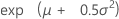 |
| Desv.Est. |
 |
| Término | Description |
|---|---|
| μ | Parámetro de escala |
| σ | Parámetro de forma |
Distribución gamma
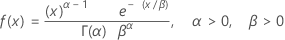 |
|
| CDF |
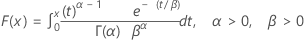 |
| Media | αβ |
| Desv.Est. | αβ2 |
| Término | Description |
|---|---|
| α | Parámetro de forma |
| β | Parámetro de escala |
Distribución exponencial
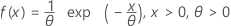 |
|
| CDF |
 |
| Media | θ |
| Desv.Est. | θ |
| Término | Description |
|---|---|
| θ | Parámetro de escala |
Distribución de valor extremo más pequeño
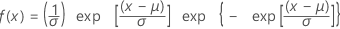 |
|
| CDF |
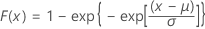 |
| Media |
 |
| Desv.Est. |
 |
| Término | Description |
|---|---|
| μ | Parámetro de ubicación |
| σ | Parámetro de escala |
| γ | Constante de Euler (aproximadamente igual a 0.5772) |
Distribución de Weibull
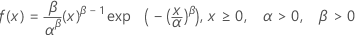 |
|
| CDF |
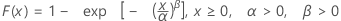 |
| Media |
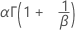 |
| Desv.Est. |
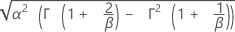 |
| Término | Description |
|---|---|
| α | Parámetro de escala |
| β | Parámetro de forma |
Distribución de valor extremo más grande
 |
|
| CDF |
 |
| Media |
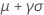 |
| Desv.Est. |
 |
| Término | Description |
|---|---|
| μ | Parámetro de ubicación |
| σ | Parámetro de escala |
| γ | Constante de Euler (aproximadamente igual a 0.5772) |
Distribución logística
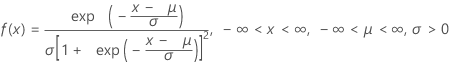 |
|
| CDF |
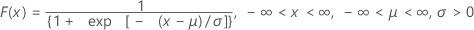 |
| Media | μ |
| Desv.Est. |
 |
| Término | Description |
|---|---|
| μ | Parámetro de ubicación |
| σ | Parámetro de escala |
Distribución loglogística
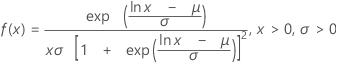 |
|
| CDF |
 |
| Media |
 |
| Desv.Est. |
 |
| Término | Description |
|---|---|
| μ | Parámetro de ubicación |
| σ | Parámetro de escala |
