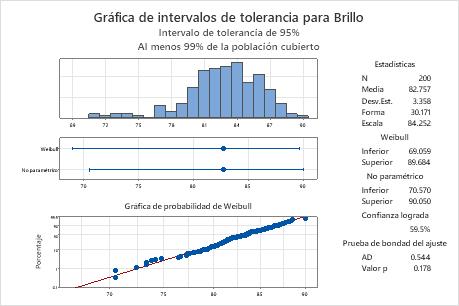
Un fabricante desea evaluar la variabilidad de su proceso de blanqueo del papel. El fabricante recoge 200 muestras de pulpa de forma aleatoria y registra el nivel de brillo. El fabricante desea calcular un rango dentro del cual se pueda esperar que se encuentre el brillo de al menos 99% de los lotes.
- Abra los datos de muestra, BrilloPulpa.MWX.
- Elija .
- En Variables, ingrese Brillo.
- En Porcentaje mínimo de población en el intervalo, ingrese 99.
- Haga clic en Aceptar.
Interpretar los resultados
La gráfica de probabilidad muestra que los puntos graficados se encuentran a lo largo de la línea ajustada de la distribución de Weibull, lo que indica que los datos siguen una distribución de Weibull. Además, el valor p de la prueba de bondad de ajuste es 0.178, que es mayor que el nivel de significancia de 0.05. Puesto que usted no puede concluir que los datos no siguen la distribución de Weibull, puede utilizar el intervalo para la distribución de Weibull.
El intervalo de Weibull va desde aproximadamente 69.1 hasta 89.7, así que el fabricante puede estar 95% seguro de que al menos el 99% de todos los lotes de pulpa estarán dentro de este intervalo. Para todos los lotes de pulpa, el nivel medio de brillo es aproximadamente 82.8.
Método
| Distribución | Weibull |
|---|---|
| Nivel de confianza | 95% |
| Porcentaje de población en el intervalo | 99% |
Estadísticas
| Variable | N | Media | Desv.Est. |
|---|---|---|---|
| Brillo | 200 | 82.757 | 3.358 |
Parámetros de distribución
| Variable | Forma | Escala |
|---|---|---|
| Brillo | 30.171 | 84.252 |
Intervalo de tolerancia de 95%
| Variable | Método de Weibull | Método no paramétrico | Confianza lograda |
|---|---|---|---|
| Brillo | (69.059, 89.684) | (70.570, 90.050) | 59.54% |