En este tema
Gráfica de corridas
Una gráfica de corridas representa los datos de su proceso en el orden en que se recolectaron. Utilice una gráfica de corridas para buscar patrones o tendencias en los datos que indiquen la presencia de variación por causas especiales.
Interpretación
Patrones en sus datos indican que la variación se debe a causas especiales que se deben investigar y corregir. Sin embargo, la variación por causas comunes es una variación inherente o una parte natural del proceso. Un proceso es estable cuando solamente las causas comunes, no las causas especiales, afectan la salida del proceso. Si solo existen causas comunes de variación en su proceso, los datos exhiben un comportamiento aleatorio.
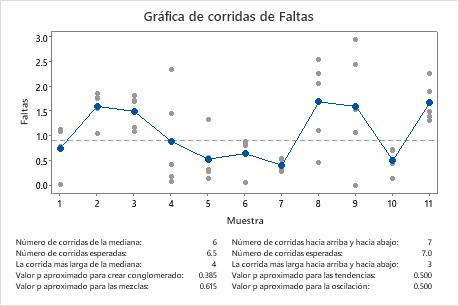
Número de corridas alrededor de la mediana
El número de corridas alrededor de la mediana es el número total de corridas por encima de la mediana y el número total de corridas por debajo de la mediana.
Una corrida alrededor de la mediana es uno o más puntos consecutivos en el mismo lado de la línea central. Una corrida termina cuando la línea que conecta los puntos cruza la línea central. Una nueva corrida comienza con el siguiente punto graficado.
Interpretación
- La corrida 1 incluye el punto 1.
- La corrida 2 incluye los puntos 2 y 3.
- La corrida 3 incluye los puntos 4, 5, 6 y 7.
- La corrida 4 incluye los puntos 8 y 9.
- La corrida 5 incluye el punto 10.
- La corrida 6 incluye el punto 11.

Número de corridas esperado alrededor de la mediana
El número de corridas alrededor de la mediana esperado es el número de corridas que usted esperaría tener en sus datos si los datos estuvieran distribuidos aleatoriamente.
Interpretación
Compare el número esperado de corridas con el número real de corridas. Más corridas de lo esperado podría indicar que los datos provienen de dos poblaciones (mezclas). Menos corridas de lo esperado podría indicar conglomerados de los datos. Utilice los valores p para probar la significancia estadística.

La corrida más larga alrededor de la mediana
El número de puntos en la corrida más larga por encima o por debajo de la media. Un punto que se ubica en la línea central pertenece a la corrida por debajo de la media.
Interpretación

Valor p aproximado para conglomerados
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula.
Utilice el valor p para determinar si los datos están distribuidos aleatoriamente. La hipótesis nula es que los datos están distribuidos aleatoriamente.
Interpretación
Un valor p que es menor que el nivel de significancia especificado indica una tendencia a conglomerados. Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que existe un patrón no aleatorio, cuando en realidad los datos están distribuidos aleatoriamente.
- Valor p ≤ α: Las diferencias de las medias son significativamente diferentes (Rechaza H0)
- Si el valor p es menor que o igual al nivel de significancia, usted rechaza la hipótesis nula. Usted puede concluir que los datos no están distribuidos aleatoriamente.
- Valor p > α: La diferencia en las medias no es significativamente diferente (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, usted no puede rechazar la hipótesis nula. Usted no tiene suficiente evidencia para concluir que los datos tienen patrones no aleatorios. Sin embargo, tampoco puede concluir que los datos están distribuidos aleatoriamente.

Valor p aproximado para mezclas
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula.
Utilice el valor p para determinar si los datos están distribuidos aleatoriamente. La hipótesis nula es que los datos están distribuidos aleatoriamente.
Interpretación
Un valor p que es menor que el nivel de significancia especificado indica una tendencia a mezclas. Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que existe un patrón no aleatorio, cuando en realidad los datos están distribuidos aleatoriamente.
- Valor p ≤ α: Las diferencias de las medias son significativamente diferentes (Rechaza H0)
- Si el valor p es menor que o igual al nivel de significancia, usted rechaza la hipótesis nula. Usted puede concluir que los datos no están distribuidos aleatoriamente.
- Valor p > α: La diferencia en las medias no es significativamente diferente (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, usted no puede rechazar la hipótesis nula. Usted no tiene suficiente evidencia para concluir que los datos tienen patrones no aleatorios. Sin embargo, tampoco puede concluir que los datos están distribuidos aleatoriamente.

Número de corridas hacia arriba o hacia abajo
El número de corridas hacia arriba o hacia abajo es el conteo total de corridas hacia arriba y hacia abajo en sus datos.
Una corrida hacia arriba es una corrida ascendente de puntos consecutivos que solo aumenta. Una corrida hacia abajo es una corrida descendente de puntos consecutivos que solo disminuye. Una corrida termina cuando la dirección (hacia arriba o hacia abajo) cambia. Por ejemplo, cuando el valor anterior sea menor, una corrida hacia arriba comienza y continúa hasta que el valor anterior sea mayor que el siguiente punto, entonces empieza una corrida hacia abajo.
Minitab cuenta una corrida plana de observaciones equivalentes consecutivas como parte de una corrida hacia abajo.
Interpretación
- El Punto 2 marca el final de la Corrida 1.
- El punto 5 marca el final de la Corrida 2.
- El Punto 6 marca el final de la Corrida 3.
- El Punto 7 marca el final de la Corrida 4.
- El Punto 8 marca el final de la Corrida 5.
- El Punto 10 marca el final de la Corrida 6.
- El Punto 11 marca el final de la Corrida 7.

Cómo interpretar una corrida plana
3 corridas hacia arriba y hacia abajo
1 corrida hacia abajo
Número de corridas hacia arriba o hacia abajo esperado
El número de corridas hacia arriba o hacia abajo esperado es el número de corridas que usted esperaría tener en sus datos si los datos están distribudios aleatoriamente.
Interpretación
Compare el número esperado de corridas con el número real de corridas. Más corridas de lo esperado podría indicar oscilación en los datos. Menos corridas de lo esperado podría indicar una tendencia en los datos. Utilice los valores p para probar la significancia.

La corrida más larga hacia arriba o hacia abajo
El número de puntos en la corrida más larga hacia arriba o hacia abajo.
Interpretación

Valor p aproximado para tendencias
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula.
Utilice el valor p para determinar si los datos están distribuidos aleatoriamente. La hipótesis nula es que los datos están distribuidos aleatoriamente.
Interpretación
Un valor p que es menor que el nivel de significancia especificado indica una propensión a tendencias. Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que existe un patrón no aleatorio, cuando en realidad los datos están distribuidos aleatoriamente.
- Valor p ≤ α: Las diferencias de las medias son significativamente diferentes (Rechaza H0)
- Si el valor p es menor que o igual al nivel de significancia, usted rechaza la hipótesis nula. Usted puede concluir que los datos no están distribuidos aleatoriamente.
- Valor p > α: La diferencia en las medias no es significativamente diferente (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, usted no puede rechazar la hipótesis nula. Usted no tiene suficiente evidencia para concluir que los datos tienen patrones no aleatorios. Sin embargo, tampoco puede concluir que los datos están distribuidos aleatoriamente.

Valor p aproximado para oscilación
El valor p es una probabilidad que mide la evidencia en contra de la hipótesis nula. Las probabilidades más bajas proporcionan una evidencia más fuerte en contra de la hipótesis nula.
Utilice el valor p para determinar si los datos están distribuidos aleatoriamente. La hipótesis nula es que los datos están distribuidos aleatoriamente.
Interpretación
Un valor p que es menor que el nivel de significancia especificado indica una tendencia a oscilación. Por lo general, un nivel de significancia (denotado como α o alfa) de 0.05 funciona adecuadamente. Un nivel de significancia de 0.05 indica un riesgo de 5% de concluir que existe un patrón no aleatorio, cuando en realidad los datos están distribuidos aleatoriamente.
- Valor p ≤ α: Las diferencias de las medias son significativamente diferentes (Rechaza H0)
- Si el valor p es menor que o igual al nivel de significancia, usted rechaza la hipótesis nula. Usted puede concluir que los datos no están distribuidos aleatoriamente.
- Valor p > α: La diferencia en las medias no es significativamente diferente (No puede rechazar H0)
- Si el valor p es mayor que el nivel de significancia, usted no puede rechazar la hipótesis nula. Usted no tiene suficiente evidencia para concluir que los datos tienen patrones no aleatorios. Sin embargo, tampoco puede concluir que los datos están distribuidos aleatoriamente.

