En este tema
Paso 1: Ver el ajuste de la distribución normal
Utilice las gráficas de probabilidad normal para evaluar el grado en que los datos originales y transformados siguen la distribución normal.
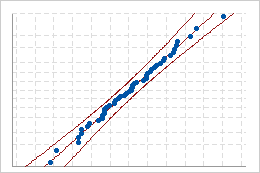
Ajuste adecuado
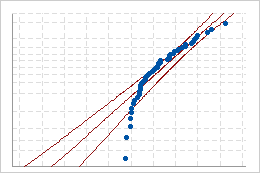
Ajuste deficiente
Nota
Si los datos originales están normalmente distribuidos, Minitab muestra solo una gráfica de probabilidad individual y no realiza la transformación de Johnson.
Paso 2: Evaluar el ajuste de la distribución normal
Utilice el valor p para evaluar si usted puede presuponer que los datos originales y transformados siguen la distribución normal.
- Un valor p que es menor que alfa indica que la distribución normal no provee un ajuste adecuado.
- Un valor p que es mayor que o igual a alfa indica que no hay suficiente evidencia de un ajuste de distribución deficiente. Usted puede presuponer que los datos siguen la distribución normal.
Si la transformación de Johnson es efectiva, el valor p de los datos transformados es mayor que alfa.
Important
Interprete los resultados de una muestra muy pequeña o muy grande con precaución. Si tiene una muestra muy pequeña, una prueba de bondad de ajuste pudiera no tener suficiente potencia para detectar alejamientos significativos de la distribución. Si tiene una muestra muy grande, la prueba pudiera tener tanta potencia que detecte alejamientos incluso pequeños de la distribución que no tengan significancia práctica. Utilice las gráficas de probabilidad, además de los valores p, para evaluar el ajuste de distribución.
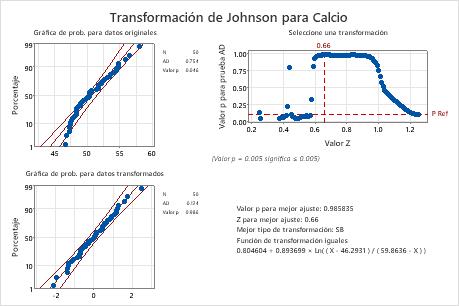
Resultado clave: Valor p
En estos resultados, el valor p (0.046) de los datos originales es menor que alfa (0.10), lo que indica que los datos originales sobre calcio no son normales. Para los datos transformados, el valor p (0.986) es mayor que alfa. Por lo tanto, usted puede presuponer que los datos transformados siguen una distribución normal.
Paso 3: Examinar la función de transformación
Minitab muestra los parámetros de la función de transformación de Johnson que produce el mejor ajuste. Minitab utiliza esta función para transformar los datos originales.
Por ejemplo, supongamos que la función de transformación de Johnson es 0.762475 + 0.870902 × Ln(( X – 46.3174)/(59.677 – X)). Si el valor de los datos originales de X es 50, entonces el valor de los datos transformados de 50 se calcula como 0.762475 + 0.870902 × Ln((50 – 46.3174)/(59.6770 – 50)), que es igual a –0.07893.
Nota
Para almacenar todos los valores de datos transformados en la hoja de trabajo, ingrese una columna de almacenamiento cuando realice el análisis.
Para obtener más información sobre el algoritmo que utiliza Minitab para definir la función de transformación de Johnson, vaya a Métodos y fórmulas para las transformaciones en Identificación de distribución individual y haga clic en "Métodos y fórmulas para la transformación de Johnson".
